6. PASCAL’S THEOREM
|
Cross Ratio on a Line |
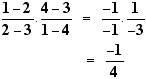 |
|
Let a, b, c, d be four lines passing through point O, and draw an arbitrary line (transversal) not through O meeting them in points A, B, C, D as in the diagram. We prove:
Proof Draw through B a line parallel to a meeting c and d in points P, Q respectively, as in the diagram. We assume that lines a and PQ are directed in the same sense. Triangles ACO, BCP are similar, so Similarly, triangles ADO and BDQ are similar, giving . Hence |
Using the adjacent diagram we have hown that the value of the cross ratio
Proof Let BB' and CC' meet in point O, and let OD meet line AB'C' in D". |
The easiest way to see this is probably to use coordinates. With the obvious notaion we have  whence we obtain d' = d". |
We first observe that in the adjacent diagram, the green pencil and the yellow pencil are actually congruent – the angles between corresponding lines are equal, using the subtending property of chords in a circle. Obviously then theses two pencils have the same cross ratio. The value of this common cross ratio is the same as the cross ratio of the points on any transversals. So we get |
Extensions 1. The cross ratio of four points on a line is worth investigating in its own right. For example, if the cross ratio is negative, what can you say about the two pairs of points? You should be able to show that the value of the cross ratio of four points remains unchanged when two pairs of points are interchanged. For looking up ... |
P
|
Hints and Solutions
1. The cross ratio of four points on a line is worth investigating in its own right. For example, if the cross ratio is negative, what can you say about the two pairs of points? You should be able to show that the value of the cross ratio of four points remains unchanged when two pairs of points are interchanged. |
 Blaise Pascal (1623 – 1662) discovered this beautiful theorem when he was just 16. Although the result seems very simple, it is hard to see where to start with a proof.
Blaise Pascal (1623 – 1662) discovered this beautiful theorem when he was just 16. Although the result seems very simple, it is hard to see where to start with a proof.  In the figure at right, a hexagon AB'CA'BC' is inscribed in a circle. (The figure shows a rather zig-zag hexagon. This is not necessary, but it makes the figure neater.) Opposite edges of the hexagon meet in points L, M and N. What appears to be true about these points?
In the figure at right, a hexagon AB'CA'BC' is inscribed in a circle. (The figure shows a rather zig-zag hexagon. This is not necessary, but it makes the figure neater.) Opposite edges of the hexagon meet in points L, M and N. What appears to be true about these points?
 Cross Ratio of a Pencil
Cross Ratio of a Pencil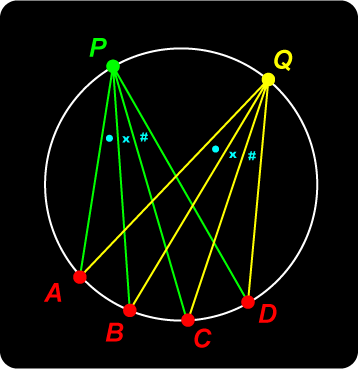 Proof of Pascal’s Theorem
Proof of Pascal’s Theorem