 |
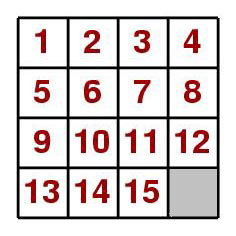
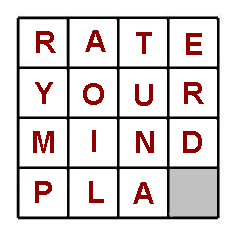
The fifteen puzzle consists of 15 square tiles which are free to slide vertically and horizontally on a 4 x 4 square tray. The tiles are numbered from 1 to 15. It can be shown that if any pair of tiles is interchanged (for example by lifting tiles 14 and 15 out of the tray and replacing them in opposite positions) then it is impossible to return the tiles to their natural order 1, 2, 3, ... , 14, 15 by sliding. In fact, any odd number of such interchanges gives rise to an impossible sliding puzzle; any even number corresponds to a solvable puzzle. Now, is it possible to slide the tiles in the second puzzle to give the message correctly? |
 |