#2           60. A TOUCHING PROBLEM                  
Do you have a problem with smoking?  

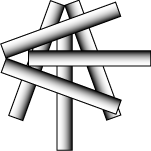
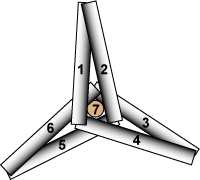
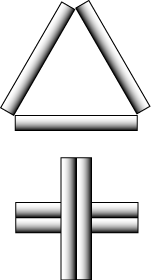
Well, here is a new and instructive use for those cigarettes!

If we take three cigarettes, we can place them in a triangle so that each one touches the other two. Similarly with four cigarettes: placing them in a cross as shown, each cigarette touches the other three.

Now, can you place six cigarettes so that each touches the other five? Expert smokers may like to try placing seven cigarettes so that each touches the other six. Both arrangements are possible.

Of course, no bending or breaking is allowed.
 Hints and strategies 

Hint                         Solution                      Extensions
HINT

Notice that the four cigarette example has a 3-dimensional solution. So, try to think of the cigarettes placed in space, rather than all lying on a plane.
HINT 2

You should have obtained remainders 6, 3, 7 for the respective departments. Also remainders 3, 2, 2, 2, 5 for F (Foster), K, P, R and W; all other names have remainder 0. You should now immediately be able to place five people in their departments.
SOLUTION

For six and seven cigarettes respectively, the solutions are:
EXTENSION

1. The mathematician would now ask whether seven was the greatest number of cigarettes with this property. What do you think?

2. The cigarette is essentially a circular cylinder. The same question can be posed for other 3-dimensional objects. Explore this possibility.