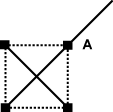
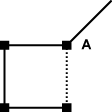
The four earliest settlers in the Hardoveering Plain built their houses one mile apart at the vertices of a square. As the years rolled by, and the telephone became a reality, the Avgerinos homestead (A) was linked to the county network by a line from the North-East. It was then decided to connect the remaining three homes. Tenders had been called and three replies received: The four earliest settlers in the Hardoveering Plain built their houses one mile apart at the vertices of a square. As the years rolled by, and the telephone became a reality, the Avgerinos homestead (A) was linked to the county network by a line from the North-East. It was then decided to connect the remaining three homes. Tenders had been called and three replies received:
Cowley Cables : $3000 The town clerk frowned as he sketched on his paper. “We know the cost of telephone cable is fixed at $1000 per mile, so it is easy to reconstruct the plans used by Cowley and Lindus. But I don’t see how Whibley can possibly do the job for that price.” Do you? |
|

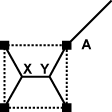 Whibley found the best solution to this shortest distance problem. In this diagram, the angles at the new points X, Y are all 120°.
Whibley found the best solution to this shortest distance problem. In this diagram, the angles at the new points X, Y are all 120°.