 Bert and his son Phil were listening to a program on the radio. Bert and his son Phil were listening to a program on the radio.
“I bore a hole through the centre of a solid sphere,” said the man on the radio. “The length of the hole when measured turns out to be 6 centimetres. Now you tell me the volume of the sphere remaining.” “That’s stupid,” said Phil. “He didn’t say what size drill he used.” “It’s not stupid,” replied the radio rather huffily. “You don’t need the size of the hole.” “He must mean that the answer is the same for any sized hole,” said Bert. “But it looks like being a complicated calculation.”
What is the volume remaining? |
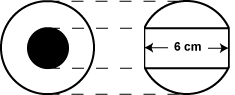

 “That depends,” answered the radio. “Maybe it’s a one-liner.”
“That depends,” answered the radio. “Maybe it’s a one-liner.”