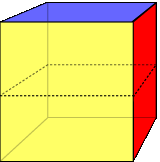
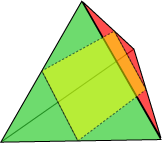
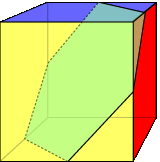
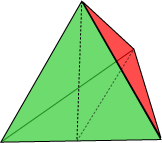
 I have just received another nuisance call from Geo. Metter. He was prattling on that he had heard it was possible to cut a regular tetrahedron into two identical pieces such that each piece had six vertices. I have just received another nuisance call from Geo. Metter. He was prattling on that he had heard it was possible to cut a regular tetrahedron into two identical pieces such that each piece had six vertices.
He couldn’t do it, and would I be able to help him since I was the fount of all knowledge and ... . I told him I would ring him back. I found it easy to obtain two identical pieces each having four vertices (see left). Six was more difficult, but after some time I managed to solve Geoff’s problem. I then wondered whether the problem generalized. Thus, it is easy to cut a cube into two identical pieces each having eight vertices. But could I obtain two identical pieces each having ten vertices? Can you solve these two problems? |
|
Hints and strategies
|