#2             93.  MYSTERIOUS MAGIC SQUARE           


The Zen of Magic Squares – Clifford Pickover


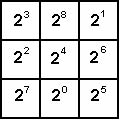
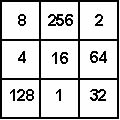
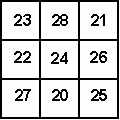The figure shows a simple magic square with the numbers in each row, each column and each diagonal adding up to 72.

The problem here is to convert this square into a multiplying magic square in which the numbers in each row, each column, and each main diagonal multiply together to give the same product.

You are not allowed to alter, or add to and of the figures in a cell, but you may shift the two figures within a cell. Thus for example, you might replace 23 by 32 in the top left-hand corner.

The puzzle appears to be extremely difficult, but look closely – it is very easy.

Hints and strategies

Hint 1                Hint 2              Solution               Extensions
HINT 1

Look closely at the magic square. Apart from its‘magic’ properties, can you see something else unusual about the numbers?
HINT 2

The given square is additive in nature. The required square is multiplicative. What do you know that links these two ideas?
SOLUTION

Write each pair as a power of 2. Each product is then 212 = 4096. Notice that 20 = 1.  Notice how the additive property used in the indices converts to multiplication. 
EXTENSIONS

You could try constructing other similar magic squares. Notice that the common magic square with single digit entries can be converted to a new magic square by adding the same multiple of 10 to each entry.

Of course the magic square does not have to be 3 x 3, but large magic squares will not convert in such a simple way, and may not convert at all.