#2             97.  IN HOW MANY WAYS?           

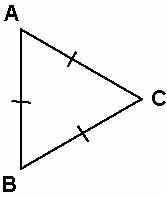
BC = CA = AB

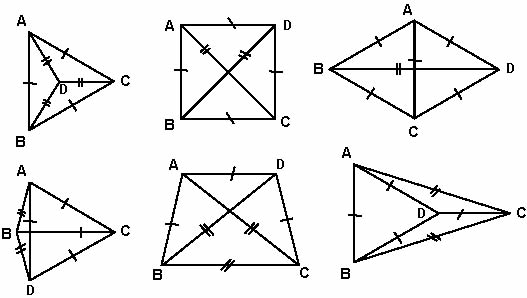
Three points A, B and C can be placed so that all the determined distance BC, CA and AB are the same.

This can be acieved in only one way – when the points are at the vertices of an equiateral triangle.

For four points A, B, C and D we get at least two different distances determined. The figure at right shows one possible arrangement.

However, this arrangement is not unique. How many other possible arrangements can you find? You may be surprised!

Notice that we are not concerned here with variations in the labelling of the points, but with different arrangements of the points.

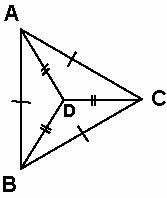
BC = CA = AB
AD = BD = CD
HINT 1

There are six determined distances. The triangle gives a three - three arrangement. What other possibilities are there?
HINT 2

Have you found six possibilities?!
SOLUTION

Surprisingly there are six possible arrangements altogether. Discovering them is largely a matter of trial, although you can try to be a little systematic in your search. You should have found:
EXTENSIONS

Increasing the number of points is an obvious way of extending this problem.

Another way is to replace the joining segments by other quantities. You might ask questions about the number of congruent triangles, ot the number of equi-areal triangles, for example.