
The kaleidoscope construction
 In the old days, before television and computer games, people had to look elsewhere for their entertainment. One source was the kaleidoscope – perhaps the best known of all optical toys. The kaleidoscope was known to the ancient Greeks, but it was rediscovered and patented in 1817 by the Scottish scientist Sir David Brewster. The name ‘kaleidoscope’ comes from three Greek words that mean ‘an instrument with which we can see things of beautiful form’. After the publication in 1819 of Brewster’s Treatise on the Kaleidoscope, the kaleidoscope became an extremely popular toy. In the old days, before television and computer games, people had to look elsewhere for their entertainment. One source was the kaleidoscope – perhaps the best known of all optical toys. The kaleidoscope was known to the ancient Greeks, but it was rediscovered and patented in 1817 by the Scottish scientist Sir David Brewster. The name ‘kaleidoscope’ comes from three Greek words that mean ‘an instrument with which we can see things of beautiful form’. After the publication in 1819 of Brewster’s Treatise on the Kaleidoscope, the kaleidoscope became an extremely popular toy.
 A kaleidoscope is made up of three inward facing mirrors forming a hollow triangle and usually placed in a long tube. One end of the tube is translucent and contains a selection of little pieces of coloured glass; the other end is covered with a hole in its center to form an eye piece. By looking through the eye piece and rotating the tube, you see beautiful changing patterns as the pieces of coloured glass tumble about and are reflected in the mirrors. A kaleidoscope is made up of three inward facing mirrors forming a hollow triangle and usually placed in a long tube. One end of the tube is translucent and contains a selection of little pieces of coloured glass; the other end is covered with a hole in its center to form an eye piece. By looking through the eye piece and rotating the tube, you see beautiful changing patterns as the pieces of coloured glass tumble about and are reflected in the mirrors.
In actual fact, for economy reasons many kaleidoscopes are manufactured with just two mirrors angled together. Different types of pattern can be obtained by varying the angle between the mirrors. The most common choice of angle is 60°, but a 90° choice is interesting. A variation on a kaleidoscope is a taleidoscope. This instrument has the same basic mirror construction, but no coloured glass, and a clear ‘far’ end. When the taleidoscope is pointed at some object, various reflections of this object form a pattern which varies as the scope is rotated.
Applet
Let us have a look at a kaleidoscope applet. This applet was created by Bob Allanson, and is based on a public domain applet constructed by Tautomu Ishikura (see
http://javaboutique.internet.com/Kaleidoscope/source.html ).
I think it is fair to say that the patterns produced by this applet are kaleidoscope-like – there is none of the rotation effect that you would get from a real kaleidoscope. However, many interesting patterns can be generated.
The ‘stop’ button will freeze the movement; the ‘start’ button will then resume the movement where it left off. Pressing the ‘restart’ button repeatedly will give a succession of new starting points. The ‘select image’ menu gives a choice of images on which the resulting patterns will be based; alternatively, you can choose one of your own. The 'show triangles' button allow you to show the underlying triangle structure of the kaleidoscope; you can choose the colours black or white. You can change the triangle size by choosing a number and then pressing return. The more mysterious 'show tiles' relates to the way in which the applet is in fact constructed – with some ingenuity!
• Look for fixed points in the patterns: all the patterns have the same set of fixed points. What can you say about the positioning of these points? To what would they correspond in the real kaleidoscope?

# The fixed points form a grid of equilateral triangles. These represent the corners where the kaleidoscope mirrors meet, and the pattern reflect across their joining lines.
Tessellations
 Squares are regular four-sided polygons which tessellate the plane: that is, they fit together, edge to edge, in a way which completely covers the plane, but with no overlappng. Squares are regular four-sided polygons which tessellate the plane: that is, they fit together, edge to edge, in a way which completely covers the plane, but with no overlappng.
• Use the applet to discover two different types of regular tessellation.
Another type of tessellation are the semiregular tessellations. These are also tessellations of regular polygons placed edge to edge, but here we allow more than one type of polygon. We insist that the polygons surround each vertex in the same way. There are in fact eight possible tessellations of this type, and they are illustrated below.
• Use the applet to see if you can discover any of the above semiregular tessellations. Some you would not expect to find in this way. Why is this?

# There are just three types of regular tessellation. Apart from the squares you might have discovered:
 |
 |
|
Triangles
|
Hexagons
|
# Because of the construction of the standard kaleidoscope, we would probably only expect to get tessellations involving equilateral triangles and regular hexagons (unless the original motif pattern had, for example, squares).
It is easy to see that there are just three possible regular tessellations. For there must be at least three polygons meeting at each vertex. Further, the interior angles of the regular polygons are 60° (triangle), 90° (square), 120° (hexagon), and more than this for the rest. Since the total angle at a vertex is 360°, we deduce that these are the only possibilities.
Isometries
An isometry is a transformation which preserves lengths (distances). [From the Greek: iso equal, same; metron measure.] Any object which is mapped by an isometry has an image which is congruent to the original: it has the same size and shape.
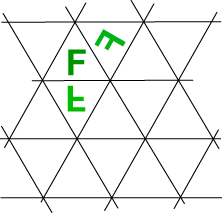
 A simple example of an isometry is a reflection in a line. Thus in the diagram at right, the letter F is reflected in the mirror line m to give a reversed letter F. The object and its image have the same size and shape. They are equidistant from the mirror line. A simple example of an isometry is a reflection in a line. Thus in the diagram at right, the letter F is reflected in the mirror line m to give a reversed letter F. The object and its image have the same size and shape. They are equidistant from the mirror line.
It is known that there are exactly four different types of isometry in the plane, and that they can all be obtained as a ‘product’ of reflections: that is, take the original F (say) and find its image under reflection, then find the image of this image under another reflection and so on for a finite number of steps.
 • Copy the diagram at right, and sketch in the triangles the relevant images of the letter F obtained under reflections in the edges. • Copy the diagram at right, and sketch in the triangles the relevant images of the letter F obtained under reflections in the edges.
• We already have the original F and an image which illustrates reflection.
Can you find an image which is obtained from F by translation? Describe it.
Can you find an image which is obtained from F by rotation?
What is the centre and angle of this rotation?
Finally, can you find an image which is not obtained from F by any of the above isometries? Describe it.

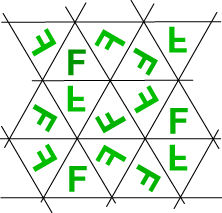 # The kaleidoscope (product of reflections) gives a pattern of Fs as shown at right. # The kaleidoscope (product of reflections) gives a pattern of Fs as shown at right.
As we have seen, there is a simple reflection in a side of the triangle immediately containing F. You should be able to see other possible reflections illustrated too. There are two examples in the figure of a translation of F. Here is one such translation. Where is the other? There are various possible rotations; here is one such rotation. The centre is marked, and the angle is a clockwise rotation of 120°. What are the others? Finally, there is one remaining isometry called a glide reflection. It is a combination of a translation and a reflection. Here is an example of a glide reflection. There is one other in the diagram.
These four isometries form a group. See for example
http://internal.maths.adelaide.edu.au/people/pscott/groups/gpf/
Notice that the identity transformation occurs as a special type of translation or rotation. We might notice two that the isometries fall naturally into two types: direct (occurring as the product of an even number of reflections) and opposite (occurring as the product of an odd number of reflections). Thus translations and rotations are direct; reflections and glide reflections are opposite.
Bibliography
General ...
http://en.wikipedia.org/wiki/Kaleidoscope
Make your own ...
http://www.csiro.au/resources/ps1up.html
Other applets ...
http://javaboutique.internet.com/Kaleidoscope/source.html
http://www.permadi.com/java/spaint/spaint.html
|

 In the old days, before television and computer games, people had to look elsewhere for their entertainment. One source was the kaleidoscope – perhaps the best known of all optical toys. The kaleidoscope was known to the ancient Greeks, but it was rediscovered and patented in 1817 by the Scottish scientist Sir David Brewster. The name ‘kaleidoscope’ comes from three Greek words that mean ‘an instrument with which we can see things of beautiful form’. After the publication in 1819 of Brewster’s Treatise on the Kaleidoscope, the kaleidoscope became an extremely popular toy.
In the old days, before television and computer games, people had to look elsewhere for their entertainment. One source was the kaleidoscope – perhaps the best known of all optical toys. The kaleidoscope was known to the ancient Greeks, but it was rediscovered and patented in 1817 by the Scottish scientist Sir David Brewster. The name ‘kaleidoscope’ comes from three Greek words that mean ‘an instrument with which we can see things of beautiful form’. After the publication in 1819 of Brewster’s Treatise on the Kaleidoscope, the kaleidoscope became an extremely popular toy.  A kaleidoscope is made up of three inward facing mirrors forming a hollow triangle and usually placed in a long tube. One end of the tube is translucent and contains a selection of little pieces of coloured glass; the other end is covered with a hole in its center to form an eye piece. By looking through the eye piece and rotating the tube, you see beautiful changing patterns as the pieces of coloured glass tumble about and are reflected in the mirrors.
A kaleidoscope is made up of three inward facing mirrors forming a hollow triangle and usually placed in a long tube. One end of the tube is translucent and contains a selection of little pieces of coloured glass; the other end is covered with a hole in its center to form an eye piece. By looking through the eye piece and rotating the tube, you see beautiful changing patterns as the pieces of coloured glass tumble about and are reflected in the mirrors. Squares are regular four-sided polygons which tessellate the plane: that is, they fit together, edge to edge, in a way which completely covers the plane, but with no overlappng.
Squares are regular four-sided polygons which tessellate the plane: that is, they fit together, edge to edge, in a way which completely covers the plane, but with no overlappng.


 A simple example of an isometry is a reflection in a line. Thus in the diagram at right, the letter F is reflected in the mirror line m to give a reversed letter F. The object and its image have the same size and shape. They are equidistant from the mirror line.
A simple example of an isometry is a reflection in a line. Thus in the diagram at right, the letter F is reflected in the mirror line m to give a reversed letter F. The object and its image have the same size and shape. They are equidistant from the mirror line.
 # The kaleidoscope (product of reflections) gives a pattern of Fs as shown at right.
# The kaleidoscope (product of reflections) gives a pattern of Fs as shown at right.