|
 Since hexagons tessellate the plane, we look forward to some pretty dissections here. However if we try to superimpose a triangular or square tessellation where the triangles or squares have the same area as the hexagons, we are in for a disappointment: the side-lengths required are unpleasant. You can find 5-piece dissections of a triangle to a hexagon and a square to a hexagon, and a 7-piece dissection of a pentagon to a hexagon on Gavin Theobald’s site. These dissections are obtained by superimposing strips, but the strips and their placings are not obvious. Since hexagons tessellate the plane, we look forward to some pretty dissections here. However if we try to superimpose a triangular or square tessellation where the triangles or squares have the same area as the hexagons, we are in for a disappointment: the side-lengths required are unpleasant. You can find 5-piece dissections of a triangle to a hexagon and a square to a hexagon, and a 7-piece dissection of a pentagon to a hexagon on Gavin Theobald’s site. These dissections are obtained by superimposing strips, but the strips and their placings are not obvious.
Problem H1. Find a dissection of 2 hexagons to 1 triangle.
If the defining lattice triangles have side-length 1, you can easily calculate that we are looking for a triangle whose edge length is the length of 4 lattice triangle altitudes (4 3/2) – like this. Carefully drag this triangle so that its centroid lies at the common vertex of the three hexagons. Now you should be able to see the pretty 6-piece dissection of the triangle to 2 hexagons. If not, here is the triangle position, and the dissection into 3 half-hexagons and 3 kites. Now arrange these 6 pieces to fill 2 hexagons. 3/2) – like this. Carefully drag this triangle so that its centroid lies at the common vertex of the three hexagons. Now you should be able to see the pretty 6-piece dissection of the triangle to 2 hexagons. If not, here is the triangle position, and the dissection into 3 half-hexagons and 3 kites. Now arrange these 6 pieces to fill 2 hexagons.
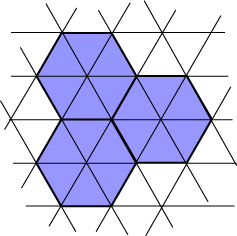
Problem H2. Find a dissection of 3 hexagons to 1 hexagon.
We use a similar method here. On the above hexagonal tessellation, superimpose a suitably sized larger hexagonal lattice. How big must it be? Well, its length must be  3: that is, the length of a non-central diagonal of one of the given hexagons. Here is such a lattice; where will we place it? Drag the red hexagon so that its centre is at the common vertex of the three blue hexagons. You should now see a simple 6-piece dissection of the 3 blue hexagons to the large hexagon. Just remove the three outward pointing blue ‘arrow’ triangles external to the red hexagon, and use them to fill the uncoloured gaps in the red hexagon. Simple! 3: that is, the length of a non-central diagonal of one of the given hexagons. Here is such a lattice; where will we place it? Drag the red hexagon so that its centre is at the common vertex of the three blue hexagons. You should now see a simple 6-piece dissection of the 3 blue hexagons to the large hexagon. Just remove the three outward pointing blue ‘arrow’ triangles external to the red hexagon, and use them to fill the uncoloured gaps in the red hexagon. Simple!
Problem H3. Find a dissection of 7 hexagons to 1 hexagon.
We adapt the method used for Problem H2. In this (unmovable!) solution, the red hexagon can be dissected to give the 7 blue hexagons. You might like to explore this type of problem for other numbers of hexagons.
|
 Since hexagons tessellate the plane, we look forward to some pretty dissections here. However if we try to superimpose a triangular or square tessellation where the triangles or squares have the same area as the hexagons, we are in for a disappointment: the side-lengths required are unpleasant. You can find 5-piece dissections of a triangle to a hexagon and a square to a hexagon, and a 7-piece dissection of a pentagon to a hexagon on
Since hexagons tessellate the plane, we look forward to some pretty dissections here. However if we try to superimpose a triangular or square tessellation where the triangles or squares have the same area as the hexagons, we are in for a disappointment: the side-lengths required are unpleasant. You can find 5-piece dissections of a triangle to a hexagon and a square to a hexagon, and a 7-piece dissection of a pentagon to a hexagon on 
