|
12. DODECAGONS |
|
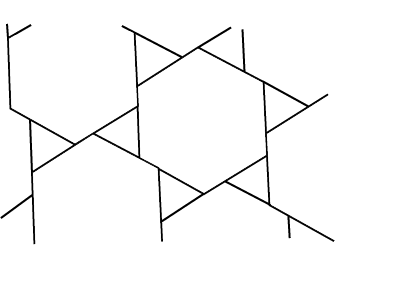
Problem D1. Find a 6-piece dissection of a dodecagon into a hexagon. An obvious place to start here is with the tessellaton of dodecagons and triangles given at right. Now perhaps we might be able to superimpose a tessellation of suitably sized hexagons and (the same sized) triangles? In fact, each hexagon here has the same area as a dodecahedron. Drag the hexagon lattice so that its lines bisect edges of the dodecagon lattice. Can you solve the problem from this? Here is the required position, and here is the solution.
Problem D2. Find a 6-piece dissection of a hexagram into a hexagon. Here we begin with the tessellation of hexagrams and triangles shown at left. We superimpose the tessellation of hexagons and triangles used above, of course taking the triangles to have the same area, and hexagram and hexagon of the same area. The orientation of the superimposed lattice is slightly different, chosen to make some of the vertices coincide. Drag the hexagon lattice so that a set of its vertices coincide with the lower vertices of the downward pointing triangles. Can you solve the problem from this? Here is the required position, and here is the solution. |
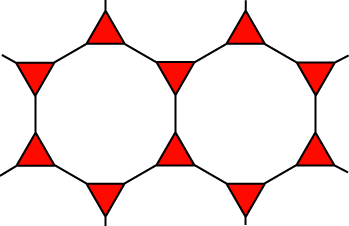 Dissections of polygons with large numbers of sides become increasingly difficult, as, with a few exceptions, the polygons do not tessellate the plane. However, the dodecahedron bears some similarity to the octahedron in that it is a component of a semiregular tessellation.
Dissections of polygons with large numbers of sides become increasingly difficult, as, with a few exceptions, the polygons do not tessellate the plane. However, the dodecahedron bears some similarity to the octahedron in that it is a component of a semiregular tessellation.