|
8. SQUARE AND TRIANGLE |
 In 1907 puzzlist Harry Dudeney discussed the dissection of a triangle to a square. He gave the rather nice 4-piece dissection illustrated at right. But where did this come from? How did he think of it? We don’t know, but we can suggest a way in which it might have been derived. In 1907 puzzlist Harry Dudeney discussed the dissection of a triangle to a square. He gave the rather nice 4-piece dissection illustrated at right. But where did this come from? How did he think of it? We don’t know, but we can suggest a way in which it might have been derived. We obviously need to start with a triangle and a square having the same area. We try working backwards, placing squares over the triangle, following the dissection lines. Fairly naturally we obtain a (blue) horizontal strip of triangles, and abutting (green) diagonal strips of squares as below. Notice how the subdivided square and triangle appear in this figure. These squares form a tessellation, but not in a regular way. Since each of the illustrated squares is partitioned 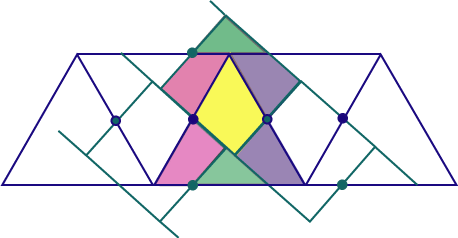 in the same way, we easily deduce that the dots are midpoints of the same-coloured segments. It follows that the area of the intersection of the triangle strip and a square strip is precisely twice the area of two triangles (squares). We shall return later to this in the same way, we easily deduce that the dots are midpoints of the same-coloured segments. It follows that the area of the intersection of the triangle strip and a square strip is precisely twice the area of two triangles (squares). We shall return later to this 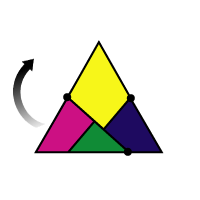 method of construction. method of construction.An interesting feature of this construction is that the pieces can form a hinged model. Folding the model one way gives the triangle; folding it the other gives the square. Try it. Step 1 : Step 2 : Step 3 : Step 0 |