|
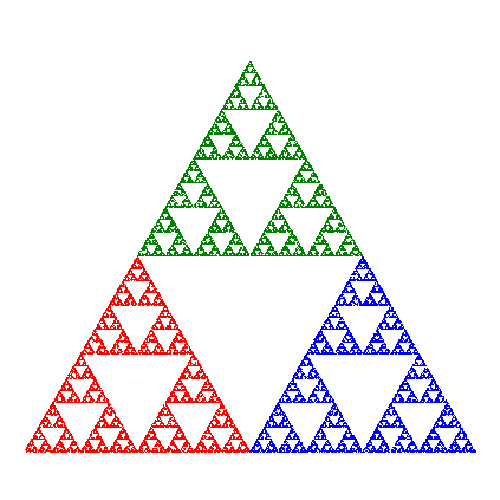
C1. SIERPINSKI TRIANGLE There is another commonly occurring class of fractals which does not appear to coincide with any of our previous classes. The Sierpinski triangle is well known. We take a triangle and delete the central triangle having vertices at the midpoints of the edges. We now repeat this process with each of the remaining three traingles, and so on. We finish with a fractal which is connected and which ‘covers’ a portion of the plane, in the sense that the basic pattern is repeated over a region. Some of our discrete fractals have a similar property, apart from the connectedness proviso.
|