amy glen : euler’s contribution to number theory

Euler was no stranger to cleaning up Fermat's incompleteness. Fermat (1601–1665) had asserted, among other things, that:
(1) numbers of the form

(called the n th Fermat number) are always prime; and

(2) if p is a prime and a is a positive integer not divisible by p, then

is divisible by p.
The first of these conjectures had simply been stated by Fermat, who left it unproven. In 1732, Euler set out to prove this theorem, but after several attempts he was unable to find a proof. He then tried to

disprove Fermat’s claim, and succeeded by finding that the fifth Fermat number,

= 4294967297, is divisible by 641.

For the second of these conjectures, known as Fermat's Little Theorem, Euler published a surprisingly elementary proof, in 1736, simply using mathematical induction on the natural number a. Having proved this result, Euler established a somewhat more general statement, in which he used the now well known Euler phi-function. For a positive integer n, he defined

to be the number of integers between 1 and n that are relatively prime to n. For example,

. Clearly, if p is a prime then

, and it can be proved that

where

are the distinct prime factors of n. Using this result, Euler generalized Fermat's Little Theorem by proving that if a and m are relatively prime then mdivides

. That is, if (a,m) = 1 then

. This is now known as Euler's Theorem, although the congruence notation was later introduced by Gauss in 1801. In addition to the phi-function, Euler also introduced the following arithmetic functions:
d(n) = number of positive divisors of n;

= sum of the positive divisors of n.
These functions are multiplicative in the sense that if (m,n) = 1 then f(mn) = f(m)f(n). If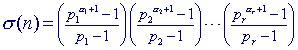

is the prime-power factorization of a positive integer n then, by the assumption of multiplicativity, Euler showed that

. This is immediately evident from the fact that the positive divisors of

are

, so that

. It is also a simple exercise to derive

.
Euler's memoir on

contains many beautiful results relating to primes and partitions. The study of such arithmetic functions allowed Euler to experiment, guess results, and verify their plausibility.