|
1. WHAT IS A LATTICE?
(a) (b) Check your answer ... |
|||
|
|
|||
|
1. WHAT IS A LATTICE?
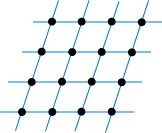
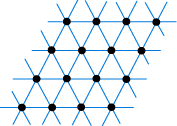
The two definitions produce the same result, but the second is more useful, because by changing the vectors we can easily obtain more general lattices such as these (in the plane):
This last is the (equilateral) triangular lattice. Transformations A linear transformation in the plane mapping point (x, y) to point (x', y') is a transformation of the type
Now, are there any linear transformations which map the integer lattice onto itself? Experiment with different integer values of (x, y) and numbers a, b, c, d. Then check your answer.
|
||||||
|
1. WHAT IS A LATTICE? A linear transformation in the plane mapping point (x, y) to point (x', y') is a transformation of the type
Now, are there any linear transformations which map the integer lattice onto itself? Experiment with different integer values of (x, y) and numbers a, b, c, d. In your experimenting, you might have found: (1) The constants a, b, c, d must all be integers. For (1, 0) maps to (a, c), and (0, 1) maps to (b, d), and each of these is assumed to be a lattice point. (2) The constants a, b, c, d must satisfy ad – bc (3) Further, for the integer lattice L to map onto itself, we require that ad – bc = ±1. For if L maps onto L, then we can undo the effect with an inverse transformation L'. Solving the equations for x', y' backwards to obtain x, y in terms of x', y' we obtain x = (dx' – by' )/(ad – bc), y = (– cx' + ay' )/(ad – bc). (*) Given that x, y are to be integral for all values of x', y', this means that ad – bc = ±1. A linear transformation x' = ax + by, y' = cx + dy with a, b, c, d integers and ad – bc = ±1 is called an integral unimodular transformation. IU Theorem A linear transformation T maps the integer lattice onto itself Proof ( ( From x' = ax + by, y' = cx + dy, since a, b, c, d are integers, it is clear that every (x', y') is a point of L. This means that L' is at least a subset of L. But does L' contain every point of L (that is, is L = L' )? Let (x*, y*) be an arbitrary point of L. We show that (x*, y*) is also a point of L'. We need to find x", y" in L such that x* = ax" + by", y* = cx" + dy". Using (*) we choose x" = (dx*– by* )/(ad – bc), y = (– cx* + ay* )/(ad – bc). (You can substitute these values in the equations for x*, y* to check.) Since a, b, c, d are integers, and ad – bc = ±1, so x", y" belong to L as required. This completes the proof. Discussion of these concepts can be found in Coxeter [C] and Hardy and Wright [HW]. Further results (1) The integer lattice can be regarded as the set of points {(x, y) = x(1, 0) + y(0,1)}. A more general lattice would be represented by {(x, y) = xu + yv} where u, v are vectors, not lying in the same straight line. With this representation, the above arguments continue to hold for the general lattice. (2) In 2 dimensions, the number ad – bc is the determinant of the matrix (3) The segment which joins A(p, 0) to B(0, p) passes through the p – 1 lattice points (1, p – 1), (2, p – 2), ... , (p – 1, 1). The p – 1 lines from these points to the origin O divide triangle OAB into p smaller triangles. The two outer little triangles contain no interior points, but Bixley and Superko [BS] show that if p is a prime number, then each of the p – 2 inner little triangles contain the same number of lattice points. (4) Two lattice points are said to be visible from one another if they can be joined by a line segment which does not pass through another lattice point. Abbot [A] shows that there is no infinite set of lattice points in the plane such that no one is visible from any other, and such that no three are collinear. Abbot also looks at the following interesting problem. Let Sn be a square array of lattice points, and let f(n) denote the least number of points in Sn such that every point of Sn is visible from at least one of the selected points. It is easily seen that f(4) = f(5) = 2. Abbot finds bounds on f(n). If S is a set of mutually visible lattice points, Rumsey [R] asks how dense S can be in the lattice. (5) In n-space, how many points of the integer lattice lie in a right simplex (triangle, tetrahedron ... ) bounded by the coordinate planes and an arbitrary plane? Lehmer [L] finds some bounds for this number. (6) Kenmitz [K] observes that if we take any set of five lattice points in the plane, then there are two such that the connecting segment is bisected by a lattice point. He extends this to general dimension. [A] Abbot, H. L., Some results in combinatorial geometry, Discrete Mathematics 9 (1974) 199 – 204. [BS] Bixley, M. T. L., Superko, C. M. Problem E1455, American Mathematical Monthly 68 (1961) 806. Also appears in the book Mathematical Morsels by Ross Honsberger, Dolciani Mathematical Expositions #3, American Mathematical Society (“Sharing Lattice Points”). [C] Coxeter, H. S. M., Introduction to Geometry, Wiley (Edition 2 1969) pages 51 – 54. [HW] Hardy, G. H., Wright, E. M., An introduction to the theory of numbers, Oxford (Edition 4 1960) pages 27 – 28. [K] Kenmitz, A., On a lattice point problem, Ars Combinatoria 16 (1983) 151 – 160. [L] Lehmer, D. H., The lattice points of an n-dimensional tetrahedron, Duke Mathematical Journal 7 (1940) 341 – 353. [R] Rumsey, H., Sets of visible points, Duke Mathematical Journal 33 (1966) 262 – 274. |
|||||
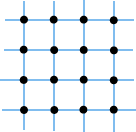 We use the word lattice or point lattice to denote a regular infinite array of points in the planes or in space. A simple example in the plane might look like this:
We use the word lattice or point lattice to denote a regular infinite array of points in the planes or in space. A simple example in the plane might look like this: