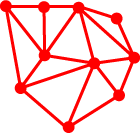
6. NON-SIMPLE LATTICE POLYGONS

Euler and Pick

Pick’s Theorem, as we have given it, applies to what are called simple polygons: polygons with a non-intersecting boundary which divides the planes into two regions – an inside (interior) and outside (exterior). We shall show that there is an extension of Pick’s theorem to a wider class of lattice polygons which we shall specify shortly.

To understand this extension, we need to realize that there is an interesting connection between Pick’s Theorem and Euler’s Formula. Suppose we have a map made up of points (vertices) which are joined by (not necessarily straight) arcs (edges) in the plane which partition the plane into non-overlapping regions (faces). There are some constraints on this map: for example, we insist that the map have at least one point, be ‘in one piece’, that the map have no ‘loops’ (an edge with two endpoints in common), and that the edges do not cross (apart from meeting at a common endpoint).

Then for such a map having V vertices, E edges and F determined faces,

V – E + F  =  2 (Euler’s Formula).

Thus for the map at left, above, V = 8, E = 11, F = 5 (including the exterior region) and

V – E + F  =  8 – 11 + 5  =  2 as required.

Euler’s Formula is easily established by induction. It is clearly true for just one point (V = 1, E = 0, F = 1). Suppose it is true for some given map, and consider the effect of adding one further edge. Either such an edge joins an existing vertex to a new vertex (so V and E are each increased by 1, and the formula is unchanged), or it joins two existing vertices (in which case E and F are each increased by 1 and the formula is unchanged). Hence Euler’s Formula is true for all planar maps.

We observe that this proof bears some similarity to the additive part of the proof of Pick’s Theorem: in each case, adding to the figure leaves the formula unchanged. Funkenbusch [F] established the connection as follows.

Suppose we have a simple polygon with B boundary points, I interior points, and triangulate it completely to obtain E edges. Then we claim that

                                           E = 3I + 2B – 3.

Thus, in the figure, E = 19, I = 2, B = 8, and 19 = 3.2 + 2.8 – 3.

This is proved by mathematical induction too.
First check that the formula holds for a simple triangle (E = 3, I = 0, B = 3).
Next assume it holds for a given triangulated polygon, and consider adding a further triangle. This can be done in one of two ways.
(a)  We can add a vertex and two adjoining edges, increasing B by 1 and E by 2.
(b) We can join two existing vertices, increasing I by 1 and decreasing E and B by 1.
The formula for E remains true for each of these operations. We deduce that the formula always holds.

Now consider Euler’s Formula: V – E + F = 2, applied to the triangulated polygon.
Let the polygon have area A. We have

                      V  =  I + B,   E  =  3I + 2B – 3,  and  (F – 1)/2  =  A.

We obtain this last formula by decreasing F by 1 to allow for the exterior region, and making the assumption that each ‘primitive’ lattice triangle has area 1/2. Substituting for V, E and F in Euler’s Formula and rearranging, gives Pick’s Formula: A = I + B/2 – 1.

Extending Pick’s Theorem

We can extend Pick’s Theorem to cover non-simple polygons. We shall assume that for our non-simple polygon P,

(a) if two edges of P intersect, their intersection is a vertex of each and so a lattice point;

(b) every boundary point belongs to a non-degenerate lattice triangle which is contained in P;

(c) the ‘area enclosed by P’ is the sum of the areas of regions which can be reached from ‘outside P’ by an odd number of crossings of the boundary (the shaded areas below).


(a)                  (b)             (c)                            (d)      

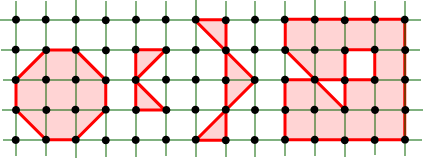
Now assuming that our polygon P has V vertices, E edges and F actual faces (that is, we don not count the exterior region), we define the Euler characteristic, P, of the polygon P by
                                                              P  =  V – E + F,
and of the boundary of P by
                                                             =  V – E .

We can now prove the
|

Extended Pick’s Theorem  The area of any lattice polygon is given by

A(P)  =  1/2B + I + k,

where k = – P  + 1/2P.

Before we establish the theorem, check out the entries in this table which refer to the four polygons pictured above.

 
B
I
P
 
k
A(P)
(a)
8
4
1
0
–1
7
(b)
5
0
1
–1
– 3/2
1
(c)
8
0
1
–2
–2
2
(d)
22
3
–1
–2
0
14

Notice that in Case (a) the value k = –1 gives the standard Pick Formula, as expected.

Proof of the Extended Pick’s Theorem

This clever proof appears in [GKW] and is quoted in Rosenholz [R].

Let P be our triangulated polygon, and let D be the ‘double’ of P : we form D by taking two copies of P and gluing them together along corresponding points of their boundaries. D is certainly a triangulated region: you might like to think of it as ‘inflated’ and lying on the surface of a sphere. We let the letters V, E and F denote the total number of vertices, edges, and faces (primitive triangles) respectively, and we use subscripts where necessary to distinguish between P and D. We now have

(1) D = VD – ED + FD   (This is the definition.)
(2) D = 2P –   (Adding the vertices, edges and faces gives a double count of vertices and edges around the common boundary; this is corrected by the second factor.)
(3)  VD = 2I + B (Obvious: two sets of interior points, and the points on the common boundary.)
(4) 2ED = 3FD (Each triangular face of D has 3 edges, but each edge belongs to 2 triangles.)
(5) FD = 2FP (By definition of D.)
(6) A = 1/2FP. (The area of P is given by multiplying the number of triangles making up P by their common area 1/2.)

Now we put it all together.

           FD = D – VD +  ED                                   by (1)

                =  ( 2 P – ) – VD +  ED           by (2)

               =  2 P – – (2I + B) + ED       by (3)

               =  2 P – – 2I – B + 3/2FD     by (4).

Hence

    1/2FD  = 2 I + B – 2 P +                   (*)

and so

         A  =  1/2FP                                                          by (6)

             =   1/4 FD                                                        by (5)

             =   I + 1/2 B – P + 1/2             by (*)

as claimed.

Rosenholz gives a discussion of the ‘obvious’ claim that primitive lattice triangles have area 1/2.

Further result

(1) If we agree to regard every boundary lattice point of polygon P as a vertex, and count the edges accordingly, we get V = B. Then using the above formula for the area A we obtain

A  =   I + 1/2 B – P + 1/2       

     =  (I + 1/2 B) – (B – E + F) + 1/2(B – E)
                                 (substituting for P ,   with  V = B)

     =  I + 1/2E – F.

Thus we obtain the interesting generalization of Pick’s Theorem:

A = I + 1/2E – F.

For simple polygons, E = B and F = 1, and we obtain the usual Pick formula. See Hadwiger and Wills [HW] (in German), and Rosenholz [R2].


References

[F]  Funkenbusch, W. W., From Euler’s formula to Pick’s formula using an edge theorem, American Mathematical Monthly 81 (1974) 647 – 648.

[GKW] Gaskell, R. W., Klamkin, M. S., Watson, P., Triangulations and Pick’s theorem, Mathematics Magazine 49 (1976), 35 – 37.

[HW] Hadwiger, H., Wills, J. M., Neuere Studien über Gitterpolygone, Journal für die reine und angewandte Mathematik 280 (1973) 61 – 69.

[R] [R2]  Rosenholz, I., Calculating surface areas from a blueprint, Mathematics Magazine 53 (1979) 252 – 256.