3. SCOTT RUSSELL LINKAGE

The Inventor

John Scott Russell was born in Glasgow in 1808. He was a Scottish naval engineer who built the Great Eastern (the largest ship built at that time) in collaboration with Isambard Kingdom Brunel, and made the discovery that gave birth to the modern study of solitons. He was made a Fellow of the Royal Society of Edinburgh (FRSE) and a Fellow of the Royal Society (FRS) of London. John Scott Russell is also remembered for a very useful linkage which carries his name, even though, by one of those quirks of historical misnaming, it is thought to have been invented by a certain William Fremantle in 1803.
The Scott Russell linkage is also called a half beam mechanism.

The Linkage

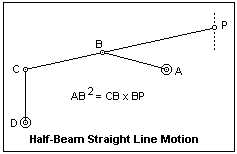A Scott Russell linkage converts linear motion, to linear motion in a line roughly perpendicular to the input.

The half-beam mechanism is shown in the figure at left. A and D are fixed pivot points. The link CD is taken to be as long as is conveniently possible, as we want C to traverse a short horizontal path. In order that P be guided on a straight line, the length of link AB should be the mean proportional between the lengths CB and BP: that is, AB² = CB x BP. Now as C moves backwards and forwards along a short straight horizontal path, the linkage makes point P move backwards and forwards along a short straight near-vertical path.

This mechanism was used on the locomotives of Wylam Colliery built by William Hedley, notably the Puffing Billy of 1813, which had vertical cylinders and drove the wheels through cranks. The engines on each side of the locomotive were 90° out of phase, to avoid dead spots, and the large half-beams above the engines had a shape and syncopated motion that was likened to that of a grasshopper’s legs, and so the engines were called ‘grasshoppers’. This name spread to the mechanism itself in later years.

The engineering design of locomotives improved over theyears and by the year 1830, the linkage straight-line motion finally disappeared. It lingered on for many years with stationary engines, especially those with vertical cylinders. It was thought for many years that horizontal cylinders would wear unevenly, a fear that turned out to be unwarranted. The main defect of the straight-line motions was their ungainly size and weight, especially for fast engines, compared to a compact slider mechanism.

Scott Rusell linkages are still used today in front wheel drive motor vehicles with solid rear axles to control lateral movement.


The Mathematics

There are several approaches to the mathematics of this problem. One is called ‘the sliding ladder problem’. A ladder leaning against a wall starts to slide, with the top of the ladder sliding down the wall, and the foot sliding out along the floor. The usual question is to find the locus of the centre of the ladder. As we shall see, t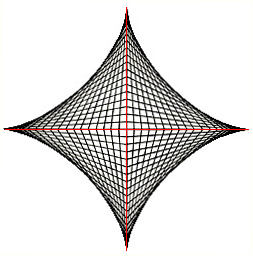his is precisely our problem here.


If the positions of the ladder are all drawn in, we obtain the first quadrant of the envelope of a curve called the astroid (pictured right). The quadrant of this interesting curve has equation

                         x^2/3 + y^2/3 = c^2/3.

Now, suppose the ladder (sliding segment) has length 1, and meets the x-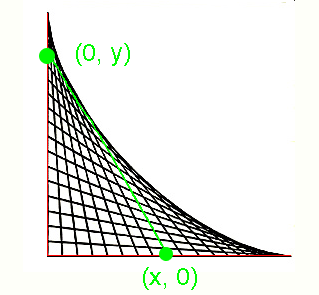axis in point (x, 0), and the y-axis in (0, y).

Clearly by the theorem of Pythagoras, x² + y² = 1.

The midpoint of the segment has coordinates (x', y') = (x/2, y/2), so the locus of the midpoint is the circle

                   x'² + y'² = 1/4.


In terms of our linkage mechanism, we see that this is precisely the situation we have: one end of the main link moving vertically, one end moving horizontally, and the centre mocing in an arc of a circle.

The Java Applet