|
5. SARRUS LINKAGE
|
||
|
The Inventor
Pierre Frédéric Sarrus, was a French mathematician who lived from 1798 to 1861. He was a professor at the Universty of Strasbourg in France, and is remembered for his work in several areas of mathematics. He was the author of several treatises, including one on the solution of numeric equations with multiple unknowns in 1842, one on multiple integrals and their integrability conditions, and one on the determination of the orbits of comets. He also discovered a mnemonic rule for evaluating the determinant of a 3 by 3 matrix, named Sarrus's rule (essentially the ‘cross product’ evaluation rule). He is of special interest to us here because of his invention of the Sarrus linkage.
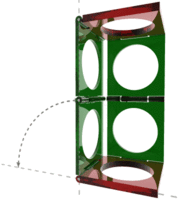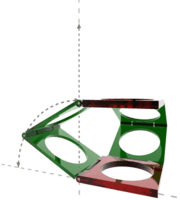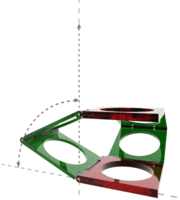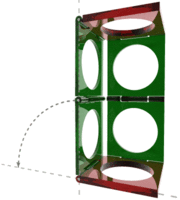
Sarrus invented his linkage in 1853. It is a mechanical linkage which converts a linear motion to a part circular motion, or vice-versa. It is a delightfully simple linkage, but it differs from our previous linkages, in that it is spatial rather than planar. The linkage uses two parallel (brown) rectangular plates positioned parallel one above the other. A vertical up and down motion moves these plates together and apart. These plates are connected by two hinged pairs of (green) rectangular plates as shown in the diagram. The movement of the parallel plates produces a circular arc motion by these hinges. The Sarrus linkage is of a three-dimensional class sometimes known as a ‘space crank’. The animation is taken from http://en.wikipedia.org/wiki/Sarrus_linkage The Mathematics
|
||
|
|
 The Linkage
The Linkage