Bicycle wheels are circular in shape. What properties of the circle make it suitable for the shape of a wheel? What if the shape were a hexagon? an ellipse? a Reuleaux triangle?

The wheel of a bicycle has 32 spokes. If we suppose that the spokes all lie in a plane and meet at the centre, then the angle at the centre between two adjacent spokes would be
Each January, The Tour Down Under is held in South Australia. Over six days, cyclists from more than 20 countries travel over 700 km, often in intense heat, in a competition involving country and city stages.
 


The important properties of the circle here are
(1) the circle has a centre, and
(2) the circle has constant width: that is, in all directions, the distance between parallel tangents (touch-lines) is the same.

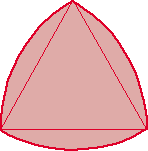
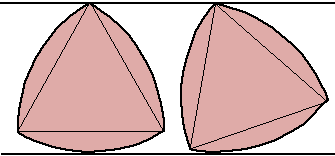
The hexagon has a centre, but not constant width. You would get a very up-and-down ride, as well as six bumps each revolution. The ellipse has a centre, but not constant width. The Reuleaux triangle has constant width, but it does not have a central point. Thus it could be used as a ‘roller’ between two parallel lines, but not as a wheel.

     


Sorry!
This doesn’t look rght at all.
Have another try.


I’m afraid not.
Think about this a bit more,
and try again.