Much interesting mathematics of the weather concerns weather forecasting. We are all familiar with the way the Weather Bureau often ‘gets it wrong’.

Information on the weather is obtained from various scattered weather stations. It is tempting to think that if there were many closely spaced weather stations, the forecasting would be accurate. But this is not the case. This is explained by chaos theory.

When a result is generated by a recurrence relationship, small errors at each step may accumulate, leading to a large inaccuracy. This is the situation with weather forecasting, where the weather at any hour depends on the weather an hour before. It has been said that a butterfly moving its wings in Africa may in time cause a tornado in the US!                     

Demonstration                   

The book Introduction to Chaos and Fractals by Peitgen, Jürgens and Saupe (Springer) gives a gentle coverage of this topic.

                                                     Forecasting               


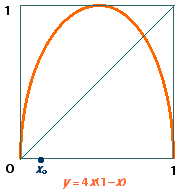
This graph is the parabola
y = 4x(1 – x).
The diagonal blue line has equation
y = x.

In the construction we begin with a point x0 on the x-axis as shown.
The vertical height is then the corresponding y-value, y0 say.

The horizontal line meets the
diagonal y = x giving x1 = y0.

We now continue the process using this x1,
drawing up to the parabola to give the value y1. ...

We thus obtain the recursive sequence of values
x0, x1, x2, ... satisfying xn+1 = 4xn(1 – xn).

Now let us repeat this taking a point close to x0.
Notice how the initial small difference
gives rise to greater and greater variation.