Granada   Andalusia, the southernmost region Spain, contains within it the legendary cities of Sevilla, Córdoba and Granada. It is also the province of oranges, olives, sunflowers and grapes, the flamenco and the bullfight, and the large resort area of the Costa del Sol. The city of Granada has a spectacular situation, set against a backdrop of the snow-capped Sierra Nevadas, Spain’s highest mountain range. It consists of the upper town, built on either side of a narrow gorge of the Rio Darro, and the lower town, where most of its quarter of a million inhabitants live. On the northern hill of the upper town lies the residential area known as the Albaicín, the old Arab quarter, and the Gypsy district of Sacromonte, while on the southern hill is the walled fortress-palace known as the Alhambra, the principal destination of the many tourist visitors. The lower town boasts many attractions of historical and cultural interest, including the Capilla Real (Royal Chapel), the mausoleum of Ferdinand and Isabella, who commissioned Christopher Columbus’s voyage to the New World, and who accepted the surrender of Spain’s last Moorish rulers here in 1492. For the sightseer, the shopper or the music lover (for this was the home of the composer Manuel da Falla), Granada is a delight.
www.sdflags.com      




z



















The Alhambra

The name Alhambra is an abbreviation of the Arabic Qal’at al-Hamra (the red fort), which aptly describes the reddish colour of the walls of this place. It was built as a fortified town within the city of Granada but separate from it, surrounded by a 2.2 kilometre wall with 22 towers and 4 main gates. Its known history began in the 11th century, but most of the palaces, towers and gardens for which the Alhambra is famous were built during the reign of Moorish rulers in the period 1238 – 1391. Following the end of Muslim rule in 1492, further building was undertaken, most notably the imposing Italianate palace of Charles V (the style of which is completely at odds with its setting). After the 16th century, the Alhambra fell into a state of decay, and restoration only began following the visit of American writer Washington Irving whose book The Alhambra (1832) aroused international interest.

For the mathematically inclined, the geometric decoration on the walls, ceilings and panels in the halls and courts of the Muslim palaces are of captivating interest: the Mexuar, the Palacio de Comares (Comares Palace) and the Palacio de los Leones (the Palace of the Lions), although there is much to admire in the Sala de Baños (Royal Baths) and the Tower of the Infantas. For the aesthetically inclined, it is the gracefulness, lightness and delicacy of the decoration itself which appeals.


































Plane patterns in the Alhambra

Because of a religious restrictions Islamic decoration was abstract. Thus, the designs and patterns in the Alhambra involve three basic non-representational forms: calligraphic (writing), vegetal (plants) and geometric (shapes). Most common are the geometric designs, based on the regular division of the circle. All constructions made use of the straightedge and compass, which the Islamic mathematicians understood very well. Thus they could divide the circle into equal (or approximately equal) parts (up to 12) with these tools, and so could construct regular (or approximately regular) polygons with n sides for n = 3, 4, ... , 12.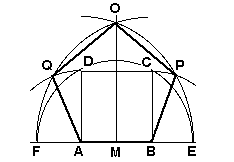 For example:

 Investigate Given AB construct square ABCD and median M(O).
   Draw arc centre M, radius MC to obtain E. Draw arc centre A,
   radius AE to obtain O. Draw arc centre B, radius AE (= BO)
   to obtain F. Draw arc centre B, radius BC (= BA) to obtain P.
   Similarly, obtain Q.
   Prove that ABPOQ is a regular pentagon.

Draw the diagonals of the regular pentagon to produce a regular pentagram. As the first steps of the above construction establish that AE:AB = 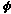:1 (why?), the ratio 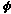:1 is to be found within the parts of the pentagram.

 Investigate What ratios within the pentagram involve 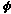? Or, consider how to construct a regular pentagon within a given circle.

























The analysis of patterns

There is no theory available about how the patterns were designed, but it is possible to gain some insight into the patterns themselves, for there are features which make the patterns amenable to analysis. The most obvious feature is the repetition of motifs based on symmetry : translational, reflectional and rotational. Underlying this is a unit of composition , most commonly the equilateral triangle, the square and the regular hexagon; less commonly, the regular pentagon, decagon and dodecagon, and other n-gons. While the patterns follow strict geometrical rules, designs were embellished with colour and ornamental highlighting (thus in fact enhancing the symmetry) and were imbued with a feeling for proportion, continuity and rhythm.

Here are three examples found in the Alhambra:

Pattern 1                      Pattern 2                     Pattern 3

 






















Alhambra pattern 1

This can be viewed as a pattern of octagonal stars, or pointed crosses, or both. Or one might see it as being generated by sets of parallel and perpendicular lines set at 45° to the horizontal, as below:

Consider the octagonal star as the major motif. It may be constructed as below from a square and its inscribed circle. It has 8 axes of symmetry through the centre of the star (1 vertical, 1 horizontal, 2 diagonal, and 4 others between these).

The octagonal star can be generated by means of two mirrors meeting at an angle of /8 at the centre of the star. Try it.

Now consider the pointed cross (right) as the major motif, constructed similar to the star.

3. How many axes of symmetry does it have? Show how this motif can be generated by a pair of mirrors meeting at a point.

   





















Alhambra pattern 2

This design can be viewed as a pattern with a leaf motif, a skew swastika (or its reflection), or both.

Or as sets of parallel and perpendicular lines set at 45° to the horizontal (below right).
The major motif of the design can be constructed from a square and its inscribed circle. Investigate the symmetries within this.




 



























Alhambra pattern 3

This pattern can be viewed as having a triangular motif with rotational symmetry, angle of rotation = 2/3.

Or as a hexagonal motif with rotational symmetry, angle of rotation /3.

Or, again, as three sets of ‘parallel’ wavy lines set at 60° to each other.
       
As it appears in the Alhambra, the basic design for Pattern 3 is embellished with a hexagon and a hexagonal star. It is best viewed as based on a hexagon whose vertices are centred in the hexagons and stars. Does this embellished design still have rotational symmetry?

 Investigate Draw this design using a ruler and compass.     
























Plane symmetry

One way to classify 2-D (wall) patterns is in terms of the symmetry groups of the plane which preserve those patterns. There are only 17 types of such groups, and all are represented in the ornamentation of the Alhambra.

The symmetry groups fall into five classes.
Here they are, with their traditional symbols.

Parallelogram net: p1, p2.
Rectangular net: p11m, p1g, p2mm, p2gm, p2gg.
Centred rectangular net: c11m, c2mm.
Square net: p4, p4mm, p4gm.
Hexagonal net: p3, p31m, p3m1,
p6, p6mm.

    
























Reflecting on the patterns

 Investigate

Look at Pattern 1 above. Satisfy yourself that its symmetry group is p4mm.

Look at Pattern 2. Is its symmetry group p11m (leaf motif), p4 (skew swastika) or p4mm (major motif)?

What is the symmetry group for Pattern 3?

 Investigate  Here are some further patterns for analysis.

[Hint: Look for the smallest region which contains all the elements of the motif. Look for centres and axes of symmetry. Tracing paper and/or a mirror may help.]

 

 



























Nets or grids

All of the Islamic wall patterns can be related to an underlying net or grid which can be used to analyze or construct the patterns. The regular tessellations, which involve congruent regular polygons, are most commonly used. There are only three of these, since the equilateral triangle, the square and the regular hexagon are the only regular polygons whose internal angles divide evenly into 360°.

Note that the arrangement of polygons around each vertex is the same for each of the regular tessellations (e.g. at each vertex of the square tessellation there are always four squares); such tessellations are said to be uniform.

 Investigate  Suppose that a tessellation includes more than one kind of regular polygon. At any vertex of such a tessellation, the number of polygons is 3, 4, 5 or 6. (Why?)  It can also be shown that each interior angle of a regular n -gon measures (n - 2)/n. (Can you prove this?) Deduce that there are eight possible tessellations if there are three regular polygons at each vertex.

These are the semi-regular tessellations.     














Further research

Anyone interested in some ideas and techniques for constructing or creating Islamic patterns should consult

Islamic Patterns, Critchlow, K., Thames and Hudson (1976).



Some web references for the Alhambra and Islamic Art are:


http://weasel.cnrs.humboldt.edu/~spain/alh/

http://tuspain.com/alhambra.htm

http://www.lacma.org/islamic_art/intro.htm