|
|
Unité d'Habitation / Marseilles Block South of the centre of the city on the Boulevard Michelet (the N559) is one of the most influential buildings of the twentieth century. It is an apartment block, known as the Unité d’Habitation, built in 1947 and designed by the great Swiss architect Charles-Edouard Jeanneret, known commonly as Le Corbusier. (He was also a painter, sculptor and city planner.) The building’s architectural significance lies in its use of raw concrete, its style of construction, and its inclusion of communal facilities (e.g. a shopping precinct and a rooftop kindergarten), features which were widely emulated, though without the same devotion to harmonious design, for high rise apartment blocks all over the world. Similar but less successful apartment blocks designed by Le Corbusier may be found in Berlin and Nantes. The mathematical significance of the Unité lies in the architect’s deliberate and overwhelming use of the Golden Section and Fibonacci Series in the design, using a system which he termed ‘The Modulor’.
|
|||||
|
Now consider a sequence of rectangles beginning with a golden rectangle (1) of unit width. Along the length of this rectangle, add a square (2) to produce a new rectangle of length 1 + |
|
Le Corbusier wanted to design mass housing for the post-World War II reconstruction which was modularised, relatively cheap and yet inhabitable. To achieve this, he argued, the proportions needed to be based on the proportions of the human body so that people would feel ‘at home’, and the measurements compatible with each other to facilitate the modular construction. |
|
The Modulor (II) Having demonstrated the constructibility of the proportions for his modular grid, Le Corbusier looked for a standard height upon which to base the Modulor. He settled on 183 cm, the height of a ‘six-foot detective’, giving 113 cm as the navel height (the dimension of the unit square), 226 cm as the height of the fingertips of the upraised arm, and 86 as the height where the hand rests. He then defined a Red Series (Rn) : 5, 11, 16, 27, 43, 70, 113, 183, 296, 479, 775, 1254, ... – Fibonacci sequences containing the key dimensions 113 and 183, 86 and 226. Allowing for rounding off, the system worked well in metric and imperial units. Using the values in the two Series, Le Corbusier was easily able to demonstrate that any square or rectangular region whose dimensions corresponded to those values could be dissected in seemingly limitless numbers of ways into smaller regions whose dimensions also took values from the Series. Here was the proportional method which would allow modularisation of components for building yet provide needed variety. He was proud to boast that in his Unité d’Habitation he only needed 15 standard measurements for the whole project, including dimensions of windows, doors, furniture etc. The Modulor system was successfully used in a whole range of other design projects, including factories, sculpture, typography and offices. |


 Attractively situated on the Gulf of Lyons just east of the Rhône delta, it is a bustling commercial and industrial centre, home to over 1 million inhabitants,
Attractively situated on the Gulf of Lyons just east of the Rhône delta, it is a bustling commercial and industrial centre, home to over 1 million inhabitants,  including a growing proportion of people of African origin who have added vigour and variety to its lifestyle. Because of its history (from around 600 B.C. when the Greeks founded a city here) and its size, Marseilles provides the visitor with much to explore. Its crowning glory is the cathedral of Notre-Dame-de-la-Garde (left).
including a growing proportion of people of African origin who have added vigour and variety to its lifestyle. Because of its history (from around 600 B.C. when the Greeks founded a city here) and its size, Marseilles provides the visitor with much to explore. Its crowning glory is the cathedral of Notre-Dame-de-la-Garde (left).
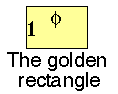 Golden section and Fibonacci sequence (I)
Golden section and Fibonacci sequence (I)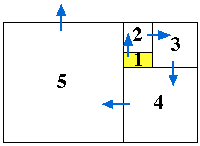 Golden section and Fibonacci sequence (II)
Golden section and Fibonacci sequence (II)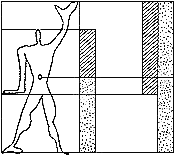 The Modulor (I)
The Modulor (I)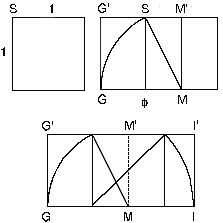 He appealed to an idea of the Ancient Greeks (and Egyptians), that the navel divides the upright body in the ratio
He appealed to an idea of the Ancient Greeks (and Egyptians), that the navel divides the upright body in the ratio