New York

New York is a brash, bustling city of over 7 million people. Known as ‘The Big Apple’, it is the acknowledged American capital of finance, theatre, art, fine cuisine, and many other things. It is famous world-wide for its dramatic skyline, the Empire State Building, and the Statue of Liberty. It has 930 km of waterfront, 10 300 km of streets, 23 km of beaches, 3500 churches and synagogues, and 200 skyscrapers. The city itself is divided into five boroughs, of which Manhattan (Island) is the chief drawcard for visitors. Lower Manhattan contains the city's main business district, including Wall street. However, following 5th Avenue northward, the vast soft green contrast of Central Park comes into view, with its trees and lakes and walkways. Located near the eastern boundary of the park is a very special museum known as ‘the Met’.   

www.sdflags.com 





































The Metropolitan Museum of Art

The Metropolitan Museum of Art is classed by art critics as one of the world’s great art museums. Its history can be traced back to 1866, but the original building in Central Park was dedicated in 1880.

It contains a vast array of art – over two million items – including ancient Egyptian, Greek and Roman exhibits, right through to contemporary art from all over the world. There are also collections of glass, armour and musical instruments. The museum itself has to be seen to be believed. Courtyards, chapels, furnished rooms – in many cases physically removed from their original locations – make the Met a source of delight and wonderment to the visitor. Don't try to see it all in one day!

Further reading ...

Hibbard, H. (1980), The Metropolitan Museum of Art, Harper and Row.
Salvadore Dali Catalogue (1980), The Tate Gallery.     































Salvador Dali

Salvadore Dali (1904–1989) began his formal art education at the San Fernando Art Academy in Madrid, Spain. He had a stormy career, and was suspended for a year. Finally he was permanently expelled after publicly refusing to take an examination, declaring ‘None of the professors of the school of San Fernando being competent to judge me, I withdraw’. He has become one of the best well-known artists of the twentieth century. He was a surrealist painter, and most of his paintings are full of strange imagery. Many of his paintings are difficult to understand; others are strangely powerful. Dali himself once remarked, ‘The only difference between me and a madman is that I am not mad'! In his later life, Dali became interested in Christian devotional themes, and from this period comes the painting featured here: Crucifixion, or Corpus Hypercubicus. It has special mathematical interest because of the geometric nature of the cross. The cross itself is made up of eight adjoining cubes. We investigate whether this configuration of cubes has any particular geometric significance.    
























A planar cross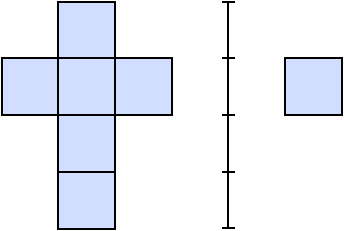

We might compare the Dali cross with a more orthodox cross, the plane face of which comprises six adjoining squares.

Notice that we would in fact obtain this plane figure by looking at the Dali cross ‘straight on’. This shape is the standard net for constructing a cube. If we now looked at this planar cross ‘edge on’ we would see four adjoining line segments. These can be thought of as a ‘net’ for a square.

The process appears to end here, for if we look at the four collinear line segments end on, we see a single point! However, the idea of dimension is clearly present. Perhaps we might get more insight by considering the constructed figures (cube, square), rather than the nets.

 Investigate Carefully draw your own 6-square cross on light cardboard. Add a small flap to every second outside edge. Cut out your shape, with flaps, and carefully fold along remaining lines. Assemble your resulting net to form a cube.

  Project  Find out about model-making. Construct your own collection of models. For example, there are five regular and 13 semi-regular polyhedra.

 






























A new approach (I)

Take a unit square and translate it 1 unit in a direction perpendicular to itself, and think of the vertices of the square leaving ‘trace paths’: we obtain a unit cube. Similarly, take a line segment of length 1 and translating it 1 unit in a direction perpendicular to itself: we obtain a square. Take a point and translate it 1 unit (perpendicular to itself!): we obtain a line segment. We thus obtain the above sequence of figures.

Can we extend this sequence beyond the cube? Thus, could we translate the cube 1 unit in a direction ‘perpendicular to itself’? This is a bit hard to visualize, but only because we live in a 3-dimensional world. Suppose we obtained a ‘4-dimensional’ cube, or hypercube by this means. What properties would such an object have?

This table lists the numbers V, E, F, ... of vertices, edges, faces, ... of the objects in the sequence. It is easy to fill in the first four columns.
Point
Segment
 Square Cube
V
E
F
1
0
0
2
1
0
4
4
1
8
12
6

 






















A new approach (II)

 Investigate   Is there a rule amongst the table entries (as in Pascal’s triangle), which will allow us to deduce the entries from those which come before?  From the given values, and the construction of the figures, find the rule. Hence add a new row (starting with C for Cell – the number of ‘3-dimensional faces’) and a new column (under Hypercube).

Point
Segment
 Square Cube Hypercube
V
E
F
C
1
0
0
__
2
1
0
__
4
4
1
__
8
12
6
__
___
___
___
___

 






















Putting it all together

Finally, we relate this 4-dim solid to the Dali cross. It is possible to represent a 3-dim solid by a plane figure — we do this all the time with photographs and paintings. However, when as here we draw a picture of a cube say, some distortion takes place: only two of the six square faces remain square. To obtain this cube from the original net, identify the inner square with the square of the net which is surrounded by four squares; the bottom square of the net is then folded up to complete the cube.

Similarly, a hypercube can be pictured as one cube placed inside another, with the corresponding vertices joined: we can do this in 3 dimensions as shown here. Here, the central cube is in fact surrounded by six other cubes, although these appear distorted because our ‘picture’ is in a lower dimension. There are thus a total of eight cubes as we expect from our table. We can now visualize how the hypercube is constructed from the net which makes up the Dali cross: the central cube is surrounded by six others as above, and the bottom cube is ‘folded up’ to enclose the others.

The title of the painting shows that Dali was aware of the significance of his cross. Perhaps he painted it this way to give an extra ‘spiritual dimension’.