|
Mysteries of the transfinite
How does one tell if two sets contain the same number of elements? The obvious answer is to ‘pair off’ the elements. Mathematically, we put the elements into a one-to-one correspondence. Thus the sets {a, b, c}, {u, v, w} have the same number of elements, since a 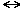 u, b u, b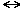 w, c w, c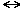 v say. This number is in fact ‘3’ because we can set up the correspondence with the integers 1, 2, 3. v say. This number is in fact ‘3’ because we can set up the correspondence with the integers 1, 2, 3.
Galileo observed that the one-to-one correspondence n 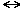 2n shows that there are equal numbers of integers (n) and even integers (2n). For, we set up the pairing ..., –1 2n shows that there are equal numbers of integers (n) and even integers (2n). For, we set up the pairing ..., –1 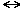 –2, 0 –2, 0 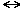 0, 1 0, 1 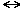 2, 2 2, 2 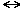 4, 3 4, 3 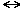 6, ... . Surprisingly, the even integers form a proper subset of the set of integers. That is, the proper subset contains just as many elements as the set itself. This characteristic of infinite sets was first properly explored by Cantor in the late 19th Century. 6, ... . Surprisingly, the even integers form a proper subset of the set of integers. That is, the proper subset contains just as many elements as the set itself. This characteristic of infinite sets was first properly explored by Cantor in the late 19th Century.
 Investigate Use the following argument to show that the number of positive fractions is the same as the number of positive integers. Investigate Use the following argument to show that the number of positive fractions is the same as the number of positive integers.
(a) List the positive fractions as in the table.
(b) Do all positive fractions occur here? all positive integers?
(c) Set up an arrow path as shown to contain all the table entries.
(d) Delete numbers like 2/2, 4/2,... which represent repeat entries.
(e) Observe that the arrow path sets up a correspondence between the table entries and the numbers 1, 2, 3, ... , the order of the terms in the sequence.
|