|
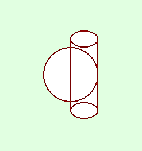 A curious curve A curious curve
Let a sphere be intersected by a cylinder, where the radius of the cylinder is half the radius of the sphere, and the side of the cylinder (the generatrix) passes through the centre of the sphere. Then the line of their intersection forms a curve known as the Viviani curve, named after the Italian mathematician Vincenzo Viviani (1622–1703).
If the radius of the sphere is unity ( = 1), then its equation is x2 + y2 + z2 = 1, and the equation of the curved surface of the cylinder is (x – 1/2)2 + y2 = 1/4.
Let P be a point on the surface of a unit sphere centred at the origin O. If r denotes the radius of the circle of latitude through the point P, the coordinates of P are
x = r cos 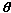 = cos = cos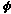 cos cos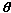 , y = r sin , y = r sin 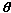 = cos = cos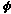 sin sin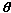 , z = sin , z = sin 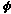 , where , where 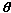 is the latitude and is the latitude and 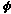 the longitude of the point. (See diagram.) the longitude of the point. (See diagram.)
 Investigate Substitute these values for x and y into the equation for the cylinder given above to find the coordinates of the points on the Viviani curve. Show that Investigate Substitute these values for x and y into the equation for the cylinder given above to find the coordinates of the points on the Viviani curve. Show that 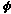 = ± = ±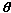 , and deduce that the points on the Viviani curve are given by , and deduce that the points on the Viviani curve are given by
x = 1/2(1 + cos 2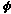 ), y = ± 1/2 sin 2 ), y = ± 1/2 sin 2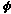 , z = sin , z = sin 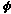 . . 
Further reading ...
|