Northamptonshire

The county of Northamptonshire is in central England just over an hour’s drive north-west of London along the M1 motorway. Its scenery is pleasant rather than spectacular: undulating wooded pasture land devoted largely to agriculture, and ideal for fox hunting. The two major towns, Northampton and Kettering, have long been associated with footwear manufacture. The county attracts the committed visitor rather than the casual sightseer, as there are no major tourist attractions.

However, around Kettering are some of the most interesting houses in England, including Rushton Hall, a Tudor house, built by the eccentric Tresham family and now used by the Royal Institute for the Blind.   

www.sdflags.com 






































Rushton Triangular Lodge

In the grounds of Rushton Hall, situated 6.5 km NW of Kettering, is the Triangular Lodge, erected in 1593 by Sir Thomas Tresham. The Lodge is an intensely pious testament to Tresham’s Catholic faith and an elaborate pun on his name and his family emblem, the trefoil.

Everything in the building is based on the number three. There are three walls, each with three gables and three triangular windows, three storeys and a three-sided chimney. The three faces, each dedicated to one member of the Holy Trinity, are each 33 feet long. Above the windows are written the 18 letters MENTES TUORUM VISITA (Visit the minds of Thy people), two letters per window, while along the top of each wall is a 33 letter passage from the Bible. Nine angels house conduits which drain water from the roof, and above the door are the words TRES TESTIMONIUM DANT (There are three that bear witness). Even the date of construction, 1593, is divisible by three. In addition, there is a fantastic array of triangles and trefoils used as decorative devices all over the building.

Buildings based on triangles or three-fold symmetry are rather rare. They include a three-sided ‘Sepulchral Church’ by British architect Sir John Soane, and the Huntingdon Hartford clubhouse by US architect Frank Lloyd Wright based on a trefoil ground plan. The modern A-frame house has a triangular cross-section, although it lacks other symmetries found in the Lodge, while the geodesic dome is constructed of triangular faces to produce a sphere-like shape.































The Tresham trefoil

 Investigate  The illustrated shaded three-fold figure is called a trefoil. The three circles meet at a point in the centre of an equailateral triangle whose vertices are the centres of the circles.

If the triangle has side length 1, what is the area of the shaded figure?

Further reading ...

http://www.britainexpress.com/History/follies.htm

Lambton, L. (1988), An album of curious houses, Chatto and Windus.

Moscovich, I. (1986), Mind benders: games of shape, Penguin.

Beard, R. S. (1973), Patterns in space, Creative Publications. 






















Triangular shapes, triangular numbers

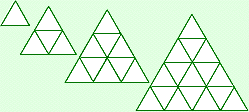
 Investigate Consider this set of shapes. Each triangular shape is made up of small equilateral triangles, a new base row of small triangles being added successively. In successive large triangles there are 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, ... small triangles. These numbers are of course the squares or square numbers 1, 4, 9, 16, ... . We are led to the slightly paradoxical situation of squares being generated by equilateral triangles. Can you explain this?

 Investigate  Next consider the vertices occurring in the above figure:
The number of dots (vertices) in successive triangular arrays is 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4, ... or 1, 3, 6, 10, ... . These are the triangular numbers, which consist of the sums of consecutive integers beginning with 1 (which has been added for completeness). Show that the nth triangular number, Tn, is n(n+1)/2.

 Investigate  Use the triangular numbers up to 100 to test the hypothesis that any positive integer up to 100 is either a triangular number or can be written as the sum of at least two (perhaps equal) triangular numbers. For example, 9 is not a triangular number, but can be written as the sum of triangular numbes 3 and 6. [Hint: There is an obvious trivial solution! Look for sums of as few terms as possible.]






















      

Patterns with triangles

Here are some designs using equilateral triangles for you to construct. The first two are flowers based on triangles growing out of a regular nonagon and a regular dodecagon. The third is the Sierpinski triangle: a large equilateral triangle is divided into four congruent equilateral triangles, and the middle one is removed. Repeat the process on each of the remaining triangles.

Pascal’s triangle

The well-known array of positive integers known as Pascal’s triangle (although its existence predated Pascal by at least 400 years) contains other triangles within it.

 Investigate  Look at the even numbers within the triangle. Extending the triangle if necessary, what triangular pattern do they make? Can you make a conjecture here? 




























Divisibility by three

As was noted previuously, the number 1593 is divisible by 3. Other than actually dividing by 3 to produce a whole number with no remainder, there is a rule which says that

a number is divisible by 3 if the sum
of its digits is divisible by 3.

Thus, since 1 + 5 + 9 + 3 = 18, which is divisible by 3, then 1593 is divisible by 3.

 Investigate  Can you prove that the above rule works for any positive integer?

[Hint: Let the positive integer be N = an10n + ... + a110 + a0. Rearrange the terms to include a multiple of 3. Now relate N to the sum an + ... + a1 + a0.]

Can you devise tests of divisibility involving multiples of 3, such as 9, 12, 15, 18 etc? There are also simple divisibility tests for division by 11 and 13. Can you find them?