The city of Bristol

Bristol may well be best known for its nearby Clifton suspension bridge which hangs like a cobweb across the Avon Gorge. However, this city of half a million inhabitants in the west of England has a long seafaring history, and still has the salty air of a sea-trading port. Any visitor will want to spend time in the harbour area, viewing the first iron-built ship, the Great Britain, and admiring the remnants of the old town which survived the bombing of World War II. The cathedral dates from 1140; it has an ornate interior with superbly carved choir stalls.

Following a few blocks north from the harbour inlet, St Augustine’s Reach, we come to a little shopping area called Christmas Steps, a steep climb up the hill. At the top is the Chapel of the Three Kings of Cologne, built in the 1480s.
www.sdflags.com 

 






































The café

Across Upper Maudun Street we come to St Michael’s Hill leading up past the University and Hospital, and on the corner a rather unattractive looking café, which has sparked a surprising amount of scientific and mathematical interest. The café is faced on the outside with tiles in two different colours. The café is situated close to the University, and in 1973 one of the university staff observed that the horizontal mortar lines between the tiles appear not to be parallel, even though they are. Rather they appear to converge quite markedly in alternating wedges. The obvious question to ask is ‘Why does this happen?’ We might also ask whether there are other similar situations where it is not true that ‘seeing is believing’!

On a lighter note, one wonders how many times the tiles were originally placed on the café wall, trying to ensure that the rows were horizontal, and the wall looked right!































The tiling

The café tiling consists of square black and white tiles placed in horizontal rows, alternately translated a small distance to the left and to the right. Surprisingly, successive horizontal mortar lines do not appear to be parallel, but rather appear to converge alternately to the left or to the right.

Another surprise is that this illusion, depends on the colour of the mortar.

Investigate Draw your own array of black and white tiles with the horizontal mortar lines drawn in (a) black (b) grey (c) white. Which picture has the most pronounced effect? Experiment with tiles and mortar of different colours.

The illusion is strongest when the tiles contrast sharply in their brightness, and when the layer of mortar is thin and intermediate in brightness. The café tiling has been likened to the Münsterberg array, named after the psychologist Hugo Münsterberg, who wrote about it in 1897. The convergence of the horizontal lines is again evident here, but weaker. Scientists are interested in understanding why the illusion occurs. They have modified the arrays, looking at small sections of them to try to isolate the cause.

Other arrays such as the kindergarten illusion are also known. The kindergarten illusion has a very powerful converging effect.






















Seeing is believing?

There are many instances where what we see (or what we believe we see!) is influenced by the context or background.

 Investigate Look at the following examples. In each case, note what your eye tells you, then use a ruler to determine the truth of the matter. Finally, think about the context: what is it that creates the illusion?

Ex. 1;  Ex 2;  Ex 3.

There are several reasons why it is dangerous to use diagrams to prove mathematical results. One is that often a diagram illustrates but one of several possible cases. Another is shown here: things which are true often do not appear to be so. Diagrams are good for helping us to understand a mathematical situation, but should not be used as a basis for a proof.

 






















This way or that way?

Another class of illusions arise because of the way we perceive 3-dimensional space. The simplest example of this is the so-called Necker cube, first named in 1832, but popularized in the late 19th Century. It is a simple skeletal cube.

 Investigate Look at the Necker cube. Which is the front face: the top left square, or the bottom right square? Can you alternate between these two perceptions? Copy and colour the cube in two ways, each time making the ‘front’ face blue.

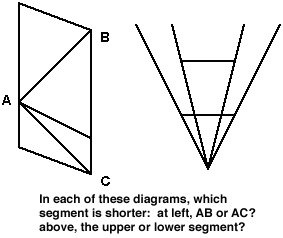
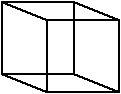
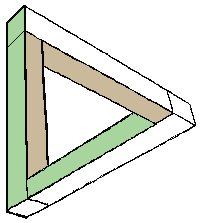
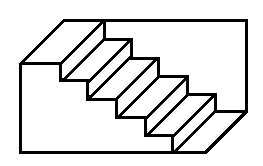The visual problem here is easily resolved by slightly modifying the edges at the two points of apparent intersection, indicating which edge lies in front. A more elaborate form of this illusion is the Schröder staircase (1858). Does the picture show the top or the underside of the stairs?

 




























Impossible figures

Closely related to the above illusions are the so-called impossible figures. Perhaps the best known is the impossible triangle, described by Penrose and Penrose in the British Journal of Psychology in 1958.

Investigate Look carefully at this figure. Why is it called ‘impossible’? Try covering up different portions of the figure. Is the part that you can still see ‘impossible’? Can you devise a way of taking a (trick!) photograph of an impossible triangle?

In the impossible triangle and other similar illusory figures, the component parts are completely realistic, but they are joined in an ‘impossible’ way. Here are some more examples:
 example 1;  example 2;  example 3;  example 4.

The artist Maurits Escher incorporated impossible figures and optical illusions into many of his works. Of particular interest in this regard are ‘Waterfall’, ‘Belvedere’ and ‘Ascending and descending’.