DUALS AND COMPOUNDS

    What are dual polyhedra?

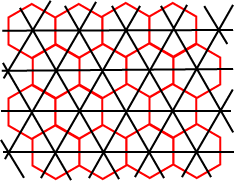You might remember that when we investigated regular and semiregular tessellations, we defined the dual tessellations. These could be defined in one of two ways:

• Join the centres of adjacent faces

• Draw the mediators (perpendicular bisectors) of the edges.

So in the figure, the dual of the hexagonal lattice is the (black) triangular lattice, and the dual of the triangular lattice is the hexagonal lattice. Notice that both methods work in each case.

We shall see that similar techniques apply to our polyhedra, the only difference being that now the second method gives a scaled up version of the dual obtained by the first method. When drawing the mediators of the edges for polyhedra, we have to be a little more specific, as the mediator is not uniquely defined. We choose the mediator which makes equal angles with the faces adjoining the edge being considered. An equivalent idea is to choose the mediator which is tangent to the midsphere of the polyhedron. Recall that this sphere touches each edge at its midpoint.

So, the dual or reciprocal polyhedron of a given polyhedron is the polyhedron obtained by either of the above methods.

  What are compound polyhedra?

In the case of the tessellations, the triangular and hexagonal tessellations separately are the duals. However, we can draw them together to illustrate their relationship and to form a pretty pattern! We can do the same with the polyhedra. Two dual polyhedra can be placed together, both for illustration and as a model. Such a compound of two polyhedra is an example of a compound polyhedron.

However, compound polyhedra can occur in many other ways. In theory, there are an infinite number of compound polyhedra, but we shall restrict our attention to the few which have pleasing symmetry properties. These are based on the nice inscribing properties we have previously investigated. Thus the two tetrahedra compound at right makes an attractive model, but there are no obvious symmetry relationships.

• Take time to think back over the work we have done so far with the Platonic solids. Think about the situations where one polyhedron has been inscribed within another. Was it possible to do the inscribing in more than one way? If so, would the set of inscribed polyhedra make a nice compound polyhedron? (We might expect some symmetry to exist in this situation.)

The compound polyhedra make lovely models, and are well worth the effort needed for their construction. Studying these polyhedra helps us to appreciate in new ways their interlinking properties.

  References