|
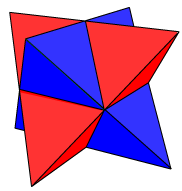
STELLA OCTANGULA
If we construct the dual of a regular tetrahedron by constructing the mediators of the edges, we obtain another congruent tetrahedron. The two tetrahedra fit together in a nice symmetric way as shown.
We notice that in the construction • the number of red edges is the same as the number of blue edges, since there is a one-to-one correspondence between them; Because the values of V and VD ( = 4), E and ED ( = 6), F and FD ( = 4) coincide, and the vertex and face values are also equal, it is difficult to discern a general pattern here from the numbers. The above argument indicates that here we might logically expect V = FD, E = ED, and F = VD. Since the dual of the regular tetrahedron is again a regular tetrahedron, we say that the tetrahedron is self-dual. We could write: the dual of {3, 3} is again {3, 3}. The illustrated polyhedron is called the stella octangula. It is the compound of a regular tetrahedron and its dual.
Although this is a very simple compound, it makes an attractive model. For nets and instructions on making this model, check out this link.
Spend some time playing with the applet, and enjoying this beautiful compound polyhedron. Use the applet to check out the following statements:
All the above statements are true. If we take all pairs of points in a given set S, and connect them with straight line segments, then the set of points of S together with all the points on the line segments form a convex set C called the convex hull of S. Of course, if S is convex, then it coincides with its convex hull. In the case above, the cube C is the convex hull of the stella octangula S. The three square cross sections are mutually orthogonal, and determine the octahedral intersection. We could think of forming the stella octangula by starting with this octahedron, and adding a triangular pyramid to each face. Another way of thinking of this, is to extend the faces within their face planes until they meet with adjacent extended faces. This is an example of stellation which we will consider later.
Since we can take the cube to have vertex coordinates ( (1, 1, 1), (–1, –1, 1), (1, –1, –1), (–1, 1, –1)
The points where the edges of the two tetrahedra meet are the centres of the square faces of the cube:
(
Johannes Kepler, who lived from 1571 to 1630 was a famous German astronomer and mathematician. He is most famous for being the first person to correctly explain planetary motion, thereby becoming the founder of celestial mechanics. Kepler also published work on the regular solids. This included recognition of duality and the idea of a combination of two tetrahedra which he called a stella octangula. This was described in his Harmonices Mundi (1619), the name being Kepler's Latin term for an eight-pointed star. It is both the simplest regular polyhedral compound, and the simplest non-convex uniform polyhedron – that is, a polyhedron with vertices all alike.
The title ‘real life’ is becoming rather a misnomer, but here are some unexpected occurrences. References MathWorld: http://mathworld.wolfram.com/StellaOctangula.html Wenninger, M., J., Polyhedron Models, Cambridge (1971), p37. |
| V | E | F | V – E + F |
|
14
|
36
|
24
|
2
|
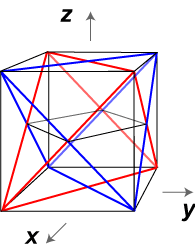 • Use your knowledge of the coordinates of the cube to find the coordinates of
• Use your knowledge of the coordinates of the cube to find the coordinates of 
