THE KEPLER – POINSOT POLYHEDRA

  Definition and notation

When we looked at the regular polyhedra, we insisted that the polygonal faces be regular and convex. Let us now consider the possibility that the polygonal faces be regular but non-convex.

The resulting Kepler-Poinsot [pwun'-soh] polyhedra are non-convex polyhedra with intersecting non-convex face planes. They were unknown to the ancient Greeks. Johannes Kepler  (right) (1571 – 1630) discovered two of them and described them in his work Harmonice Mundi in 1619. These two solids were subsequently rediscovered by Louis Poinsot (left) (1777 – 1859), who also discovered the other two, in 1809. There are in fact exactly four solids of this type. As shown later by the French mathematician Cauchy [co'-shee], they are stellated forms of the dodecahedron and icosahedron. We shall explore this as we investigate each solid. Technically they are regular polyhedra, and with the five Platonic solids, bring the number of regular polyhedra up to nine.

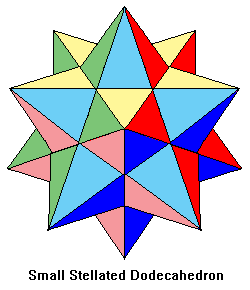
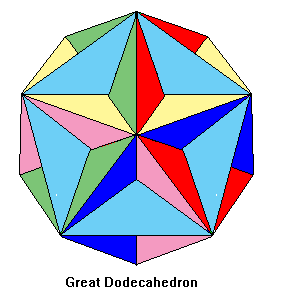
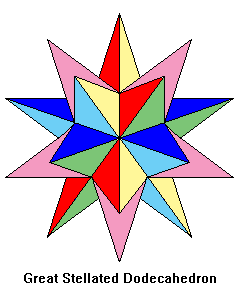
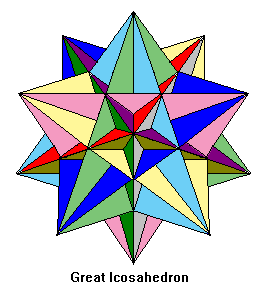
The four beautiful Kepler-Poinsot solids, illustrated below, are known as the small stellated dodecahedron, great dodecahedron, great stellated dodecahedron, and great icosahedron. These names probably originated with Arthur Cayley, who first used them in 1859. Cauchy (1813) proved that these four exhaust all possibilities for regular star polyhedra.

We shall find that the top two polyhedra, the small stellated dodecahedron and the great dodecahedron fail to satisfy Euler’s formula, V – E + F = 2, where V is the number of vertices, E the number of edges, and F the number of faces, despite the fact that the formula holds for all ordinary polyhedra. This unexpected result led the mathematician Schläfli to erroneously conclude in 1860 that they could not exist.

References