SMALL STELLATED
DODECAHEDRON

{⁵/₂, 5} or (⁵/₂)⁵

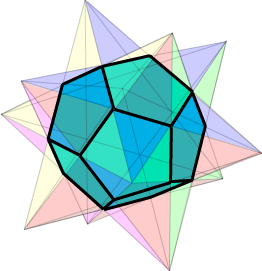
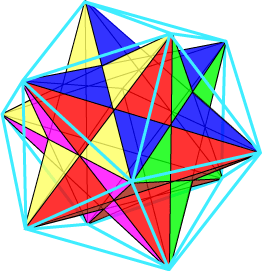
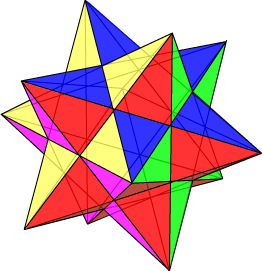
  Definition and notation

Our first Kepler-Poinsot polyhedron is the small stellated dodecahedron, illustrated at right. Kepler originally called it the echinus (the Latin for hedgehog or sea urchin), because of its prickly shape.

To understand the structure of this solid better, we need to recognize that it is based on the regular dodecahedron. Look carefully at this until you feel you understand it.

We are now going to determine the number of vertices, edges and faces. Because of the different nature of this solid, particularly its non-convex nature, our previous methods are not going to be much help. In determining the number of faces, remember that it is the whole pentagonal stars that make up the faces here, not the individual parts. Similarly, the vertices of the solid are where the (five) vertices of the pentagram faces meet. And the edges are the long line segments joining the vertices.

• How many faces, edges, vertices does it have? Can you explain the symbols above?
   Complete the table below (# stands for ‘number of’). Do you notice something strange about your last entry?

V	# pentagram faces, F	E	V – E + F

Check your answers ...

   You should have obtained:

V	# pentagram faces, F	E	V – E + F
12	12	30	– 6

Since each pentagonal star is centred on the face of the inscribed 12-faced regular dodecahedron, F = 12. Similarly, the solid is constructed by adjoining a five-sided pyramid to each face of the inscribed dodecahedron. This tells us that the number of vertices of the solid is also 12. For the edges, our previous counting method still works. Each of the 12 faces has five edges, giving a count of 5 x 12; since each edge is counted twice in this calculation, we deduce that E = 30. We observe that this is quite different from the number obtained by Euler’s formula. But then, we really have no expectation that Euler’s formula would be valid here; it is difficult to imagine how one might construct a meaningful Schlegel diagram.



  Stellations

Consider the central dodecahedron in the adjacent figure. This solid has pentagonal faces. Take one of these, F, and consider the five surrounding pentagonal faces which have an edge in common with this face. Extending each of these faces in space, beyond the boundaries with F, we see that they meet in a point ‘beyond’ face F. This happens for each face of the original dodecahedron. The new solid obtained from the original dodecahedron in this way is called a stellation of the dodecahedron. The word ‘stellation’ is related to star (as in stellar, or constellation).

  Further properties

As with the Platonic solids, we can use this Java applet to play with each of the Archimedean solids. Perhaps you can find some interesting new property! It is not impossible: new results are being discovered in elementary geometry even today. The only reason they have not been discovered before is that no-one thought to ask the right question.

• Start with the central dodecahedron, and highlight the face colours one at a time. Notice how each pentagon extends to a pentagram of the same colour.

•  See if you can make a touching circuit of three pentagrams.

• Explore how the faces of this solid occur in parallel pairs, with the faces relatively related by a half turn.

• See if you can find any further interesting properties. If you can, notify the author!

  Model making

The model of the small stellated dodecahedron is easy to make. See this construction page for some details.

  Vertex coordinates

It is a simple matter to derive a set of vertex coordinates for the small stellated dodecahedron. For, as the figure at right shows, these vertices are just the vertices of a regular icosahedron. Hence from our previous work, we can take the 12 vertex coordinate sets to be:

( , 1, 0 ),  (0, , 1 ),  (1, 0, ).

References