POLYGONS

  What is a polygon?

Our first topic is polygons. You will have some idea about what a polygon is.

• Try to define the term carefully, writing your answer in the spaces below.

Now look at the following figures. Which of these do you think are polygons?  Which are allowed by your definition? Do you want to change it?!

  (a)               (b)              (c)            (d)           (e)

The delight of mathematics is that we can define our terms how we like. But it is helpful if everyone used the same definitions. Here we would probably want to exclude figure (a) because it is not closed (doesn’t link up), and the figure (c) because of the curved arc. We will allow the other three.

Definition: A polygon is a finite set of (straight) line segments A1A2, A2A3, ... , An–1An, AnA1 (n 3) in the plane. The points A1, A2, ... , An–1, An are the vertices of the polygon. The line segments are called edges or sides of the polygon.

Figure (e) is an example of a convex polygon – it has no re-entrant angles. Figures (b) and (d) are non-convex polygons. Figure (b) is described as a self-intersecting polygon.

The word ‘polygon’ comes from the Greek: poly + gonos = many angled.
What is a regular polygon?

• Write down the conditions you think are required for a polygon to be regular.

Now look at the polygons illustrated below. Which ones are regular? Are these the ones determined by your conditions?

     (a)       (b)           (c)            (d)           (e)    

A polygon is said to be equilateral if all its sides have the same length.
A polygon is said to be equiangular if all its angle are the same size.
A polygon is regular if it is both equilateral and equiangular.

So Figure (a), the equilateral triangle, is equilateral, equiangular, and regular. It is the only polygon for which either of the equilateral and equiangular conditions implies the other. The square (b) is also equilateral, equiangular and regular, as is the pentagram (e). The vertices of the pentagram are the five outer points. The rectangle (c) is equiangular, but not equilateral or regular. the rhombus (d) is equilateral, but not equiangular or regular.

A convex regular polygon with n sides is often denoted by {n}. In these pages we shall be mostly concerned with regular polygons.
What size are the angles of a convex regular polygon?

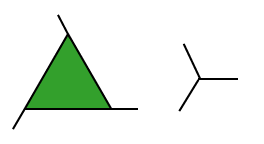Any convex regular polygon has obvious (equal) interior angles. If we move around the polygon in an anti-clockwise direction, extending each edge a short distance, we obtain a set of equal exterior angles. It is easiest to calculate the exterior angles.

• Look at the adjacent equilateral triangle. What size is each exterior angle? What is the sum of the exterior angles? Can you see why this is so? Check your answer by viewing the triangle, the square. Write your answers here:

What would be the external angle for a regular pentagon? a regular n-gon?

We obtain the sequence in radians, 2/3, 2/4, 2/5, ... , 2/n,

or in degrees, 360/3 = 120°, 360/4 = 90°, 360/5 = 72°, ... , 360/n °.

• It is now easy to obtain the size of the interior angles. What is the relationship between an interior angle and an exterior angle?



Clearly the interior angle of a regular n-gon measures – 2/n, or (n – 2)/n radians. Checking this value for the triangle, square, pentagon, ... gives /3, /2, 3/5, etc. as expected.