|
POLYTOPES
In our study so far, we have studied polygons and polyhedra. You will know that a polygon is a 2-dimensional object : it requires a 2-dimensional plane to lie in. A polyhedron on the other hand is a 3-dimensional object: it lies in 3-dimensional space. If we drop back to one dimension (a line), the closest we can get to a polygon is a line segment. In one dimension, there is only a single point. So, our definition of polytope is that a polytope is a general member of the sequence : point, line segment, polygon, polyhedron, ... . Of course, the implication here is that the sequence extends beyond polyhedron, which raises the whole question of higher dimensions! For mathematicians, this is not a problems, but it may be if you have never come across the idea before. So let us ask:
In one of his books, W.W. Sawyer imagines us talking to an angel, by which he means some being who has no actual experience of what it is like on earth. We are trying to get across the idea of dimension. We start with a dot or a point, conveying the meaning of this with some difficulty, and claim that this has dimension 0. We now agree with the angle to move this dot in a constant direction, tracing out a straight line. The angel after all knows about rays of light! We say that this straight line has dimension 1. We next struggle to explain ‘perpendicular’, but then say that a straight line moving perpendicular to itself traces out a plane which has dimension 2. Then a plane, moving perpendicular to itself traces out space which has dimension 3. We then stop, but the angel is disappointed. He asks why we can't continue to dimensions 4, 5 , 6 ... ? Of course we know that we live in a 3 dimensional world, but the angel does have a point (which is where we started!). Another way to approach this idea is using coordinates. On a straight line, the position of any point is represented relative to a given ‘origin’ by a single coordinate A fly is buzzing around a rectangular room. Within the room at any given fixed time t, we can state the position of the fly as (x, y, z) relative to three perpendicular axes. But to give the position of the fly at any time at all, why not state the position as (x, y, z, t)? This leads to the science fiction idea that ‘time is the fourth dimension’, but mathematically, the fourth letter could equally well be w and stand for something else. And there is no reason why we need stop with four coordinates.
In the plane (dimension 2), the set of points distant 1 from the origin is a circle. In space (dimension 3), the set of points distant 1 from the origin is a sphere. Now what about on a line? On a line (dimension 1), the set of points distant 1 from the origin is .
Most of our work in this chapter on polytopes will be done by analogy, but we can illustrate the idea using the circle and sphere. In the plane (dimension 2), the set of points distant 1 from the origin is a circle. In space (dimension 3), the set of points distant 1 from the origin is a sphere.
On a line (dimension 1), the set of points distant 1 from the origin is a point pair – two points, distant 1 from the origin. Why not use the same definition to obtain a hypersphere in 4 dimensions? Or beyond?
It is a bit hard for us to actually ‘picture’ the hypersphere in our 3 dimensions, but we can get a fairly good idea of what it is like and how it behaves. The equation for the point pair ( The equation for the unit circle is : x2 + y2 = 1. The equation for the unit sphere is : x2 + y2 + z2 = 1. Now what do you think the equation of the unit hypersphere might be? Notice too that using the equations it is easy to establish relationships between different members of the sequence. For example if we take the unit sphere, and intersect it with the plane z = 0, we get the unit circle x2 + y2 = 1. And if we start with the unit hypersphere, and intersect it with the hyperplane(!) w = 0, we get ... ? If you want to read more about this, look up some of the following references. Abbott, E. A., Flatland, a romance of many dimensions, Dover (Edition 6) (1953). (The full text of this delightful classic is now available online: http://www.ibiblio.org/eldritch/eaa/FL.HTM .) Sawyer, W. W., Prelude to mathematics, (Dover 1982). |
 Most of our work in this section on polytopes will be done by analogy, but we can illustrate the idea using the circle and sphere.
Most of our work in this section on polytopes will be done by analogy, but we can illustrate the idea using the circle and sphere.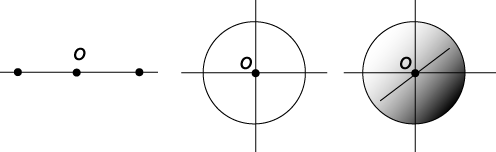 Now what about on a line?
Now what about on a line?