| |
 Definition and notation Definition and notation
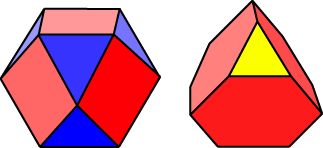 We can extend the idea of a regular polyhedron to the case where more than one regular polygon is used for the faces. In this case we have also to add a condition about the polygonal faces circling each vertex. Examples of Archimedean (or semiregular) polyhedra are shown at right. We understand that Archimedes knew about these polyhedra, although this is only inferred from the writings of others. We can extend the idea of a regular polyhedron to the case where more than one regular polygon is used for the faces. In this case we have also to add a condition about the polygonal faces circling each vertex. Examples of Archimedean (or semiregular) polyhedra are shown at right. We understand that Archimedes knew about these polyhedra, although this is only inferred from the writings of others.
An Archimedean or semiregular polyhedron is a polyhedron whose polygonal faces are regular but not all of the same type, and for which the vertex arrangements are congruent. The Archimedean polyhedra include the infinite families of prisms and antiprisms, and 13 others which we will consider in this section. Notice that the congruence of the vertex arrangements (figures) allows for reflective symmetry: all vertices do not have to have the same orientation.
The semiregular polyhedra are often denoted by a sequence of numbers corresponding to the polygons arranged about a vertex. So the figures above would be denoted 3.4.4 (triangle, square, square), and 3.6.6 (triangle, hexagon, hexagon). When using the term ‘same arrangement’ we allow clockwise or anticlockwise orientation about the vertex.
 Can we list the Archimedean solids? Can we list the Archimedean solids?
There are a number of obvious questions now. How many Archimedean polyhedra are there? What do they look like? How can we find them? How can we be sure we have all of them?
Notice that we require at least three polygons at each vertex. Also, since the equilateral triangle has the smallest vertex angle amongst the regular polygons, there can be at most five polygons meeting at a vertex (six triangles give a tessellation).
We need a strategic approach. Here is an idea.
1. Polyhedra with three polygons at a vertex
(a) Triangles, squares, ...
(b) Squares, pentagons, ...
(c) Pentagons, hexagons, ...
(d) Hexagons (We can ignore this case: three hexagons at a vertex determine the regular hexagonal tessellation.)
2. Tessellations with four polygons at a vertex
(a) Triangles, squares, ...
(b) Squares (We can ignore this case: four squares at a vertex determine the regular square tessellation.)
3. Tessellations with five polygons at a vertex
(a) Triangles, squares, ...
We could begin with a simple computer program to list the possibilities, but an alternative is to try to limit the possibilities before we start.
• (1) Suppose our polyhedron is p.q.r. (That is, each vertex is surrounded by a regular p-gon, a regular q-gon, and a regular r-gon. Can you show that if one of these numbers is odd, the other two must be equal?
(2) Suppose our polyhedron is p.q.r.s. Can you show that if one number is odd, then two of the others must be equal?
(3) Why can we ignore the configurations having all numbers equal? And the configurations 4.4.n (n  3) and 3.3.3.n? 3) and 3.3.3.n?
Check your answers ...
 We could begin with a simple computer program to list the possibilities, but an alternative is to try to limit the possibilities before we start. We could begin with a simple computer program to list the possibilities, but an alternative is to try to limit the possibilities before we start.
• (1) Suppose our polyhedron is p.q.r. (That is, each vertex is surrounded by a regular p-gon, a regular q-gon, and a regular r-gon. Can you show that if one of these numbers is odd, the other two must be equal?
(2) Suppose our polyhedron is p.q.r.s. Can you show that if one number is odd, then two of the others must be equal?
(3) Why can we ignore the configurations having all numbers equal? And the configurations 4.4.n (n  3) and 3.3.3.n? 3) and 3.3.3.n?
| Let us look at these one at a time. For (1), suppose that p is odd, and consider the polygons surrounding successive vertices of the p-gon. The adjacent polygons have to be q, r, q, ... in turn, and when p is odd, this obviously gives a problem (strictly a contradiction) when we try completing the circuit, unless q = r. See the illustration at right, but the argument holds for any odd p. In case (2) we use the same strategy, starting from top right (figure below) to add polygons around the p-gon. Again we are led to a contradiction, unless q = s. In (3) we are excluding the planar tessellations and regular polyhedra, the prisms, and the antiprisms.
Notice that in (1) and (2) the argument can be applied in turn to each odd digit. So, for example, 3.7.7 is not a possibility, as the oddness of 7 would imply equality of the other two digits.
|
 |
 |
Let us now list the possibilities remaining after we have excluded the above types:
1. 3.6.6 ; 3.8.8 ; 3.10.10 ; 4.6.6 ; 4.6.8 ; 4.6.10 ; 5.6.6 .
2. 3.4.3.4 ; 3.5.3.5 ; 3.4.4.4 ; 3.4.5.4 .
3. 3.3.3.3.4 ; 3.3.3.3.5 .
In fact, these thirteen possibilities all give rise to Archimedean solids, and we shall investigate them and their properties one by one in this section.
 Descartes’ Theorem and vertex numbers Descartes’ Theorem and vertex numbers
We came now to a simple theorem due to Descartes, which will enable us to determine easily the number of vertices of any of our Archimedean solids.
We define the angle defect at a vertex of a polyhedron to be the amount by which the sum of the angles at the corners of the faces at that vertex falls short of 2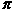 . The total angle defect of the polyhedron is defined to be what one gets by adding up the angle defects at all the vertices of the polyhedron. We call the total defect T. . The total angle defect of the polyhedron is defined to be what one gets by adding up the angle defects at all the vertices of the polyhedron. We call the total defect T.
• Consider some simple polyhedra, and determine the angle defects and the total angle defect T. Can you make a conjecture about T? Use the table below.
Check your conjecture ...
Descartes discovered that there is a connection between the total defect, T , and the Euler Number V – E + F.
Descartes Theorem. The total defect of a polyhedron and the Euler Number of that polyhedron are related by
T = 2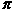 (V – E + F) . (*) (V – E + F) . (*)
This means that for any polyhedron having Euler number 2, T = 4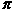 , or 720°. We shall see that while this is generally true, there are exceptions. , or 720°. We shall see that while this is generally true, there are exceptions.
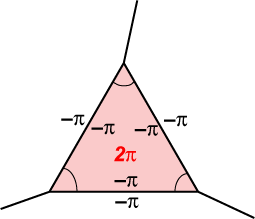 Proof of the theorem: Looking at the right hand side of (*), we can think of associating the quantity 2 Proof of the theorem: Looking at the right hand side of (*), we can think of associating the quantity 2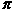 with each vertex, edge and face of the given polyhedron. Let us relate this idea to a particular face of the polyhedron. with each vertex, edge and face of the given polyhedron. Let us relate this idea to a particular face of the polyhedron.
This face contributes 1 towards the number F, so we associate 2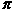 with the face. with the face.
Each edge of the face is associated with the value –2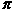 . However, each edge is shared by two faces, so with respect to the given face, we agree to associate just – . However, each edge is shared by two faces, so with respect to the given face, we agree to associate just –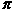 with each edge. If the edge has n faces, then the total quantity associated with the given face so far is (2 – n) with each edge. If the edge has n faces, then the total quantity associated with the given face so far is (2 – n)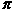 . .
We note that the sum of the angles of the polygon is in fact (n – 2)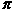 . (**) . (**)
Finally, for each vertex, we wish to allocate 2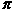 . Since each vertex is shared, we need to make a partial contribution from our given face. We agree first to give the value of the face angle at each vertex. This will be insufficient, as the angles at any vertex add to less than 2 . Since each vertex is shared, we need to make a partial contribution from our given face. We agree first to give the value of the face angle at each vertex. This will be insufficient, as the angles at any vertex add to less than 2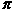 . So let us say for the given face F, the amount contributed to the total vertex count is the sum of the face angles, plus a certain composite angle defect . So let us say for the given face F, the amount contributed to the total vertex count is the sum of the face angles, plus a certain composite angle defect 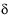 F to compensate for the shortfall. (We could define this accurately, but we are really only interested in the total defect.) F to compensate for the shortfall. (We could define this accurately, but we are really only interested in the total defect.)
So the contribution of this face to the right hand side of (*) is now 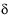 F + the sum of the angles of F + (2 – n) F + the sum of the angles of F + (2 – n)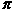 = = 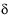 F by (**). Summing over all the faces we obtain T = 2 F by (**). Summing over all the faces we obtain T = 2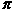 (V – E + F) = (V – E + F) = 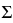 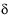 F as required, T giving the total angle defect. F as required, T giving the total angle defect.
Now what was the point of including this result? Well, for our regular and semiregular polyhedra, Euler’s formula holds, and the vertices are all alike. Hence the angle defect is the same at every vertex. This means that we now have a quick way of determining the number of vertices, even for quite complicated polyhedra. Thus
For example, the cube has angle defect 90°. Hence the number of vertices is 720/90 = 8. Yes!
 The Archimedean solids The Archimedean solids
We shall see that the Archimedean solids fall naturally into three subclasses. This classification is not exact, but it is helpful. The subclasses are
(i) the truncated group of five polyhedra, in which the vertices of the Platonic solids are removed or truncated;
(ii) the cubocta group of four polyhedra, which are easily seen to be based on the cube and octahedron; and
(iii) the icosadodeca group of four polyhedra, based on the dodecahedron and icosahedron.
|
 We can extend the idea of a regular polyhedron to the case where more than one regular polygon is used for the faces. In this case we have also to add a condition about the polygonal faces circling each vertex. Examples of Archimedean (or semiregular) polyhedra are shown at right. We understand that Archimedes knew about these polyhedra, although this is only inferred from the writings of others.
We can extend the idea of a regular polyhedron to the case where more than one regular polygon is used for the faces. In this case we have also to add a condition about the polygonal faces circling each vertex. Examples of Archimedean (or semiregular) polyhedra are shown at right. We understand that Archimedes knew about these polyhedra, although this is only inferred from the writings of others.

 Proof of the theorem: Looking at the right hand side of (*), we can think of associating the quantity 2
Proof of the theorem: Looking at the right hand side of (*), we can think of associating the quantity 2