|
1. COMPLEX NUMBERS 
|
The history of the complex numbers is very interesting. By the 16th Century, although no-one understood exactly what a complex number was, it was found that complex numbers were a useful tool for solving problems. Later, mathematicians tried to understand the complex numbers. This led in turn to investigations of the real numbers, the rational numbers, the integers and finally the natural numbers. So historically there was a reverse development: the more complicated system was found to be useful early on, and the study of the simplest systems were left till later.
|
Leibniz (1702) described complex numbers as ‘that wonderful creation of an ideal world, almost an amphibian between things that are and things that are not’.
|
Complex numbers are defined as ordered pairs z = (x, y) of real numbers x and y. We shall define addition and multiplication of these numbers shortly.
We identify the pairs (x, 0) with the real numbers x. This means that the real numbers can be thought of as a subset of the complex numbers.
Complex numbers of the form (0, y) are said to be pure imaginary numbers. The numbers x and y are now called the real and imaginary parts of z respectively, and we write x = Re z, y = Im z.
Equality Two complex numbers are equal if they have the same real and imaginary parts. Thus
(x1, y1) = (x2, y2) if and only if x1 = x2, y1 = y2.
Sum and Product The sum z1 + z2 and product z1.z2 of z1 = x1 + y1 and z2 = x2 + y2 are defined by:
(x1, y1) + (x2, y2) = (x1 + x2, y1 + y2),
(x1, y1).(x2, y2) = (x1x2 – y1y2, x1y2 + x2y1).
This last definition looks pretty weird, but we shall shortly see the reason for it.
With these definitions of addition and multiplication, we have
(x, y) = (x, 0) + (0, 1)(y, 0).
The set of complex numbers of the form (x, 0) act just like the real numbers R. Further, setting i = (0, 1) gives z = (x, y) = x + iy, and we have
i 2 = (0, 1).(0, 1) = (–1, 0), that is, i 2 = –1.
Addition and multiplication can now be rewritten as the more usual:
(x1 + iy1) + (x2 + iy2) = (x1 + x2) + i(y1 + y2),
(x1 + iy1).(x2 + iy2) = (x1x2 – y1y2) + i(y1x2 + x1y2).
1. Why did we not just start here? Notice that our derivation of i is firmly based on the real numbers. There is no ‘magic’ about 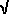 (–1), contrary to the use of the historical word ‘imaginary’. (–1), contrary to the use of the historical word ‘imaginary’.
2. We can now perform complex operations by treating the terms as real, and substituting i 2 = –1.
| Example:
(2 + 3i) + (4 + 5i) = (2 + 4) + (3 + 5)i = 6 + 8i,
and
(2 + 3i) . (4 + 5i) = (2.4 + 3i.5i) + (2.5i + 3.4i)
= (8 – 15) + (10 + 12)i = –7 + 22i.
|
The complex numbers behave in much the same way as the real numbers.
In particular they form a field. Some of the laws satisfied are:
z1 + z2 = z2 + z1; z1z2 = z2z1;
(z1 + z2) + z3 = z1 + (z2 + z3); (z1z2)z3 = z1(z2z3);
z1(z2 + z3) = z1z2 + z1z3.
These are easily proved by writing the z s in the form x + iy and using the corresponding properties of the real numbers.
We now use the idea of inverse to define division of complex numbers in the following way: z1/z2 = z1 . z2–1 (z2 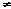 0). 0).
Try writing this out in terms of the real and imaginary parts! Later we shall give an easier way of dividing complex numbers. Clearly division by zero is not allowed, as z2–1 is undefined when z2 = 0.
The expressions below follow from this definition:
As mentioned earlier, complex numbers (like the reals) form a field, C. However, it is not possible to order C. Thus expressions like z > 0, z1 < z2 are meaningless unless the complex numbers are real.
We set up the natural correspondence z = x + iy 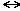 (x, y) between the complex number z and the point (x, y) in the cartesian plane. Each complex number corresponds to exactly one point in the plane, and conversely. For example, 1 + 2i is represented by the point (1,2). Notice how this corresponds to our original ‘ordered pair’ definition of a complex number. We can think of the complex number z either as the point (x, y) or as the vector from the origin to this point. (x, y) between the complex number z and the point (x, y) in the cartesian plane. Each complex number corresponds to exactly one point in the plane, and conversely. For example, 1 + 2i is represented by the point (1,2). Notice how this corresponds to our original ‘ordered pair’ definition of a complex number. We can think of the complex number z either as the point (x, y) or as the vector from the origin to this point.
The plane of such representative points is called the Argand diagram, or the complex plane or the z-plane.
The x-axis is called the real axis and the y-axis is called the imaginary axis.
|
|
Sum and Difference; Modulus
|
 |
 |
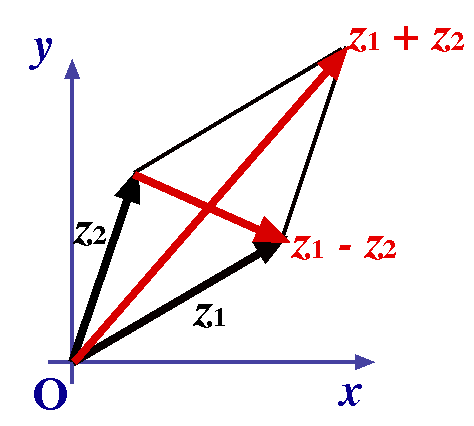 We now have an immediate geometric interpretation of the sum and difference of two complex numbers: We now have an immediate geometric interpretation of the sum and difference of two complex numbers:
Notice the direction of the arrow representing z1 – z2.
The modulus or absolute value of a complex number z = x + iy is defined to be | z |= 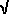 (x2 + y2). When y = 0, z is real, and we have the usual absolute value of a real number. (x2 + y2). When y = 0, z is real, and we have the usual absolute value of a real number.
The (real) number |z| denotes the length of the vector representing z, or the distance of the point (x, y) from the origin O. Even though z1 < z2 is meaningless, we can note that |z1| < |z2| is a valid statement, meaning that z1 is closer to the origin than z2.
We can extend this idea to see that | z1 – z2 | = 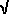 {(x1 – x2)2 + (y1 – y2)}2 {(x1 – x2)2 + (y1 – y2)}2
is the distance between the points representing z1 and z2.
Example: What is the locus of points z satisfying | z – i | = 3 ?
We are looking at points z which are distant 3 from the fixed point i. That is, a circle of radius 3 and centre i = (0,1).
If we expressed z = x + iy, then | z – i |=3 becomes the equation of this circle:
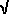 {x2 + (y – 1)2} = 3, {x2 + (y – 1)2} = 3,
or x2 + (y – 1)2 = 9.
|
The complex conjugate or conjugate of z = x + iy is the number z = x – iy. The number 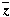 is represented in the complex plane by the point (x, –y) – the reflection in the x-axis of the point representing z. is represented in the complex plane by the point (x, –y) – the reflection in the x-axis of the point representing z.
We observe that for all z,  = z and | = z and | 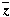 | = | z |.} | = | z |.}
|
|
More Properties of the Conjugate
|
 |
 |
The following properties are easy to establish from the definitions:
The relation z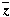 = | z |2 quickly gives = | z |2 quickly gives
| z1.z2 | = | z1 |.| z2 |, | z1/z2 | = | z1 | / | z2 |.
It is also not too hard to derive the Triangle Inequality:
| z1 + z2 |.gif) | z1 | + | z2 |. | z1 | + | z2 |.
|z1 + z2 + z3|  |z1 + z2| + |z3| |z1 + z2| + |z3|  |z1| + |z2| + |z3|. |z1| + |z2| + |z3|.
|
|
More on the Triangle Inequality
|
 |
 |
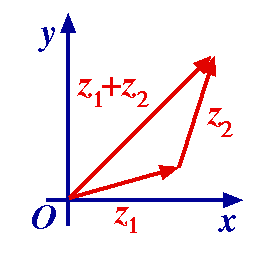 The triangle inequality becomes clear when seen geometrically, as in the adjacent figure. It just says that the length of any side of a triangle is not more than the sum of the lengths of the remaining two sides. The triangle inequality becomes clear when seen geometrically, as in the adjacent figure. It just says that the length of any side of a triangle is not more than the sum of the lengths of the remaining two sides.
Another useful result is the ModDiff Inequality:
| |z1| – |z2| | .gif) |z1 + z2|. |z1 + z2|.
We can think of this as providing a lower bound for |z1 + z2|.
Proof: |z1| = |(z1 + z2) + (–z2)|  |z1 + z2| + |–z2| |z1 + z2| + |–z2|
so |z1| – |z2|  |z1 + z2|. |z1 + z2|.
Similarly, |z2| – |z1|  |z1 + z2|, giving the required result. |z1 + z2|, giving the required result.
We say that z = (x, y) has polar coordinates (r, 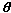 } when x = r cos } when x = r cos 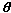 , y = r sin , y = r sin 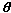 . .
We write
Note that r = |z|. We write 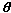 = arg z – the argument of z. The argument is always expressed in radians. We can find = arg z – the argument of z. The argument is always expressed in radians. We can find 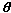 from the relationship tan from the relationship tan 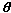 = y/x. = y/x.
The angle \theta is not unique: thus 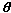  2k 2k is equally valid. is equally valid.
We use Arg z to denote the value of arg z satisfying – < arg z < arg z   . This is the principal value of the argument. . This is the principal value of the argument.
If z = 0, arg z is undefined. We adopt the convention that if z is expressed in polar form, then z 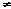 0. 0.
We begin with a natural extension: z – z0 = cis 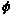 . Here, r = |z – z0|, and . Here, r = |z – z0|, and 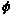 = arg (z – z0). = arg (z – z0).
The adjacent figure illustrates the situation.
The polar form is important because it gives a very simple method of multiplying and dividing complex numbers. This is because
arg (z1.z2) = arg z1 + arg z2 (*)
We shall prove this shortly, but notice that this relation may fail for the principal value ‘Arg’.
|
|
Proof of the Argument Identity
|
 |
 |
We now prove the identity (*):
arg(z1z2) = arg z1 + arg z2.
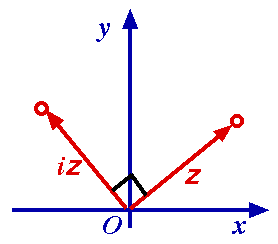
Euler’s Formula is:
We will justify this later. But note that
 We can use complex numbers to represent geometric transformations in the plane, and we shall develop this idea later. We can use complex numbers to represent geometric transformations in the plane, and we shall develop this idea later.
But as an example, consider the mapping z  f(z) = iz. f(z) = iz.
Here we have |i| = 1, arg i =  /2. So /2. So
That is, multiplication of z by i effects a rotation through  /2. /2.
This is the Engineers’ j - operator.
By induction, it is easy to obtain
where there are n factors on the left.
Equivalently, we have the well-known de Moivre's Theorem:
(cis 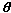 )n = cis n )n = cis n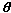 . .
(Feel free to work with either form.)
| Example: Solve zn = 1.
Since rncis n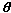 = 1, we have = 1, we have
r = 1, cos n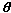 = 1, sin n = 1, sin n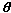 = 0 = 0  n n = 2k = 2k . .
The distinct solutions are given by
z = cis (2k / n), k = 0, 1, ... , n – 1. / n), k = 0, 1, ... , n – 1.
These are called n th roots of unity.
If wn = cis (2 / n), the n roots are / n), the n roots are
1, wn, wn2, ... , wnn – 1. Note that wnn = 1.
|
The cube roots of 1 occur as the vertices of an equilateral triangle on the unit circle.
|
|
|
Regions in the Complex Plane
|
 |
 |
We have already mentioned the complex plane. We look at some terms which describe certain sets in the plane.
A neighbourhood or more specifically, an  - neighbourhood of z0, is the set of points satisfying |z – z0| < - neighbourhood of z0, is the set of points satisfying |z – z0| <  . That is, it is the set of points lying inside, but not on, the circle of radius . That is, it is the set of points lying inside, but not on, the circle of radius  centred at z0. centred at z0.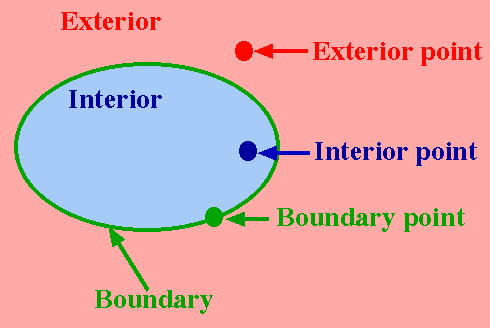
A point z is said to be interior to set S if there is some neighbourhood of z which just contains points of S. A point z is said to be exterior to set S if there is some neighbourhood of z which contains no points of S. A point z is said to be a boundary point of set S if every neighbourhood of z contains points in S and points not in S.
All the boundary points together make up the boundary of S. Notice that a boundary point of S need not be an actual point of S.
|
|
Open, Closed and Connected
|
 |
 |
A set is open if it contains none of its boundary points. In fact, this is the same as saying that every point of S is an interior point.
A set is closed if it contains all of its boundary points. Of course a set need not be open or closed. An example would be the ring 1 < |z|  2, which includes its outer boundary, but not the inner bounding circle. 2, which includes its outer boundary, but not the inner bounding circle.
Given any set S, we can take all the points of S together with all the boundary points of S to obtain a new closed set called the closure of S, and denoted 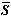 . (Not to be confused with conjugates!) . (Not to be confused with conjugates!)
An open set is connected if each pair of points of S can be joined by a polygonal path – a finite set of line segments joined end to end, which lies entirely within S.
Note You may wonder why we insisted on a polygonal path in the above definition. Why not any continuous path? The answer is that a ‘polygonal path’ is easily defined and understood. A ‘continuous path’ is a much more difficult concept.
An open, connected set is called a domain. A connected set is called a region.
Examples The disk |z| < 1, and the annulus 1 < |z| < 2 are domains. The disk |z|  1 and the annulus 1 1 and the annulus 1  |z| < 2 are regions. |z| < 2 are regions.
|
A set S is bounded if every point of S lies inside some circle |z| = R; otherwise it is unbounded.
Examples The annulus 1 < |z| < 2 is bounded (it lies inside the circle |z| = 3). The straight line {z = x + iy | y = 0} is unbounded.
|
We say that point z0 is an accumulation point of a set S, if each neighbourhood of z0 contains at least one point of S distinct from z0.
This is a more difficult concept, and is obviously associated with a limiting process. Thus we would expect to be able to find a sequence of points of S lying closer and closer to z0.
Lemma S is closed  S contains all its points of accumulation. S contains all its points of accumulation.
Proof. ( ) Let S be closed. Then S contains all its interior and boundary points. A point of accumulation of S can not be an exterior point (see the definition of exterior point). Hence S contains all its points of accumulation. ) Let S be closed. Then S contains all its interior and boundary points. A point of accumulation of S can not be an exterior point (see the definition of exterior point). Hence S contains all its points of accumulation.
( ) Suppose now that S contains all its points of accumulation. Does S contain all its boundary points? Let z0 be a boundary point of S not in S. By definition of boundary point, each neighbourhood of z0 contains a point of S, so z0 is a point of accumulation of ) Suppose now that S contains all its points of accumulation. Does S contain all its boundary points? Let z0 be a boundary point of S not in S. By definition of boundary point, each neighbourhood of z0 contains a point of S, so z0 is a point of accumulation of 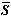 . So z0 lies in S and S contains all its boundary points. Hence S is closed. . So z0 lies in S and S contains all its boundary points. Hence S is closed.
|