5. COMPLEX
INTEGRATION PART B 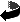
|
(BACK TO PART A)
|
|
The ‘Primitive’ Theorem: Example I
|
 |
 |
The function f(z) = z2 is entire.
 It has primitive F(z) = 1/3.z3. It has primitive F(z) = 1/3.z3.
So by our theorem,
along any contour joining 0 and 1 + i.
|
|
The ‘Primitive’ Theorem: Example II
|
 |
 |
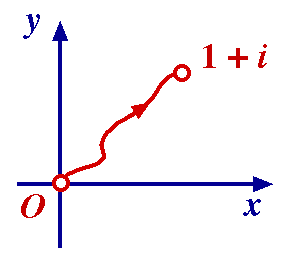
log z = ln | z | + i arg z (– /2 < arg z < 3 /2 < arg z < 3 /2). /2).
Then 
But for C2, our choice of primitive could be
log z = ln | z | + i arg z ( /2 < arg z < 5 /2 < arg z < 5 /2) /2)
and 
|
|
Simply and Multiply Connected Domains
|
 |
 |
Defintion A simply connected domain D is an open connected region such that every closed contour within it encloses only points of D. Otherwise the domain is multiply connected.
Examples
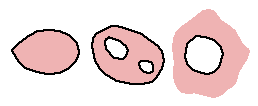
simply connected multiply connected
|
The Cauchy-Goursat Theorem has been stated for simply connected domains. i.e. if f(z) is analytic throughout a simply connected domain D, then for every closed contour C within D, 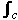 f(z) dz = 0. f(z) dz = 0.
|
|
Extending the Cauchy-Goursat Theorem
|
 |
 |
It will be useful to extend the Cauchy-Goursat Theorem to certain multiply-connected domains. Consider the illustrated (red) region D and suppose that f(z) is analytic over this (closed) region.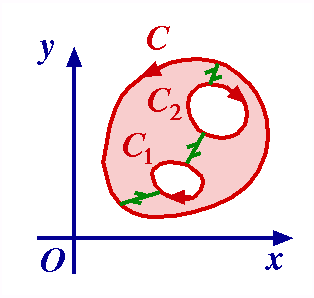
We assert that  f(z) dz = 0, where B is the total directed boundary (C f(z) dz = 0, where B is the total directed boundary (C  C1 C1 C2), with all components traversed so that the region is on the left. C2), with all components traversed so that the region is on the left.
This is easy to prove. We insert the indicated green links partitioning D into two simply-connected domains. We apply the Cauchy-Goursat Theorem to the boundaries of the left and right regions, obtaining two line integrals having value 0. Putting the two circuits together, the integrals along the introduced links cancel, giving the required result.
|
|
Multiply-Connected Domains: Examples
|
 |
 |
 Example 1 Example 1 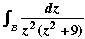 = 0 where B is the two-circle contour shown. = 0 where B is the two-circle contour shown.
For, the integrand has singularities 0,  3i, and is analytic over the enclosed domain. 3i, and is analytic over the enclosed domain.
|
|
|
The Cauchy Integral Formula
|
 |
 |
Theorem 5.3 Let f be analytic everywhere within and on a closed contour C. If z0 is any point interior to C, then
where the integral is taken in the positive sense around C.
Notes
(1) The formula is the Cauchy integral formula. It is remarkable because it gives the value of f at z0 in terms of the values of f on the boundary. That is, for an analytic function, fixing the boundary values completely determines f at points inside C.
(2) The theorem can also be used to evaluate certain integrals.
Take f(z) = z/(9 – z2), z0 = – i. Then we observe that f(z) is analytic in and on C. So using the Cauchy integral formula,
|
|
Proof of the Cauchy Integral Formula (I)
|
 |
 |
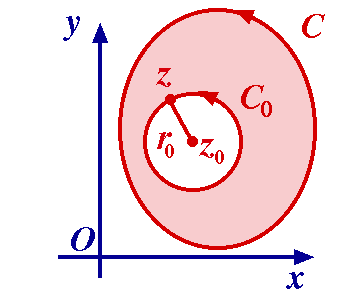 Let C0 be a circle centre z0, radius r0 interior to C. Now the function f(z)/(z–z0) is analytic at all points in and on C except at z = z0, in particular in the region D lying between C and C0. Hence as in Example 2 above Let C0 be a circle centre z0, radius r0 interior to C. Now the function f(z)/(z–z0) is analytic at all points in and on C except at z = z0, in particular in the region D lying between C and C0. Hence as in Example 2 above
where both contours are traversed in the positive direction. Hence

or I = f(z0) I1 + I2 say.
|
|
Proof of the Cauchy Integral Formula (II)
|
 |
 |
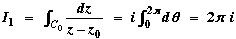 for every r0 > 0. for every r0 > 0.
Take r0 =  . Then | z – z0 | = . Then | z – z0 | = 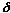 , and , and
Hence I2 can be made arbitrarily small by taking r0 sufficiently small. Since I and I1 are independent of r0, I2 must be too. Therefore I2 = 0, and
I = f(z0) I1 = 2 i f(z0). i f(z0).
|
|
Derivatives of Analytic Functions
|
 |
 |
Theorem 5.4 Suppose f is analytic inside and on a closed contour C, and z0 lies inside C. Then
That is, we can take the Cauchy integral formula and formally differentiate with respect to z0.
Proof We omit this proof. It is not unlike the proof of the Cauchy integral formula.
Note We can similarly prove:
One of most beautiful parts of course on Complex Functions is the development of
Taylor series. We look at this a little later, but for now, note the appearance here of the terms
f(n)(z0)/n!.
Example Evaluate (a)  , (b) , (b) 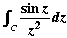 where C is the unit circle | z | = 1 taken in the anti-clockwise direction. where C is the unit circle | z | = 1 taken in the anti-clockwise direction. |
(a) Take f(z) = cos z, z0 = 0 (within C). Since cos z is entire,
I(a) = 2 i .cos z0 = 2 i .cos z0 = 2 i (the Cauchy integral formula). i (the Cauchy integral formula).
(b) Take f(z) = sin z, z0 = 0, f '(z) = cos z. Then
I(b) = 2 i f '(z0) = 2 i f '(z0) = 2 i cos 0 = 2 i cos 0 = 2 i (the Derivative formula). i (the Derivative formula).
Let us take f(z) = 1 in Cauchy's integral formula and the Derivative formulae, and let C be any contour about z0.
(a) By Cauchy's integral formula, we have
This can be rewritten as 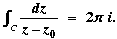
(b) By the Derivative formulae,
This can be rewritten as 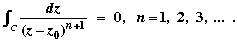
|
|
Corollary of the Derivative Formulae
|
 |
 |
If a function f is analytic at a point, then by the Derivative formulae, its derivatives of all orders are also analytic functions at that point.
Now if f(z) = u + iv, then
f '(z) = ux + ivx = vy – iuy.
So if f '(z) is analytic, then ux, vx, uy, vy are all differentiable and so continuous.
In the same way, using f "(z) etc., we see that all partial derivatives of u, v of all orders are continuous at any point where f(z) is analytic. Thus we have:
Corollary If f = u + iv is analytic at a point, then all partial derivatives of u, v of all orders are continuous there.
Note Cauchy's integral formula and the Derivative formulae easily extend to the boundaries of multiply connected domains.
Here is an interesting little result.
Lemma If f is analytic, and | f | is constant, then f is constant.
Proof Let f = u + iv. Then we are given that u2 + v2 = c.
So
2uux + 2vvx = 0, 2uuy + 2vvy = 0,
Also, by the Cauchy-Riemann equations, ux = vy, uy = –vx.
So, eliminating the u terms, we get vx2 + vy2 = 0
and so vx = 0 = vy = ux = uy.
Hence f '(z)=0 and so f(z) is constant.
Let f be analytic and not constant on the open disk | z – z0 | < r0, centred at z0. If C is any circle | z – z0 | = r (0 < r < r0) then by the Cauchy integral formula,
 (*) (*)
[Continued]
|
|
Maximum Modulus Principle
|
 |
 |
So, 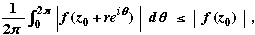 (0 (0  r < r0). (+) r < r0). (+)
Combining the two inequalities (+), we have
It follows that, | f(z) | = | f(z0) | for all z : | z – z0 | < r0.
For, write the above equation as 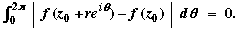
Since the integrand is non-negative, we deduce it must be 0 for all z : | z – z0 | < r0.
This shows that f(z) = f(z0) for all z in the disk. So f is constant in the disk. This is a contradiction.
Theorem 5.5 (Maximum Modulus Principle) If f is analytic and not constant in the interior of a region then | f(z) | has no maximum value in that interior.
We deduce that if a function f is continuous in a closed bounded region R and is analytic and not constant in the interior of R, then | f(z) | assumes its maximum value on the boundary of R and never in its interior.
Now let f be analytic in and on the circle C0 defined by |z – z0| = r0, and traversed in a positive sense. Then by the Derivative formulae
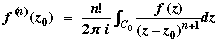 , n = 0, 1, 2, ... . , n = 0, 1, 2, ... .
If | f(z) |  M on C0, then M on C0, then
| f (n)(z0) |  n! M / r0n (n = 0, 1, 2, ...), n! M / r0n (n = 0, 1, 2, ...),
| f '(z0) |  M / r0. M / r0.
The preceding observations lead to the following theorem.
Theorem 5.6 (Liouville) If f is entire and bounded for all values of z in the complex plane, then f(z) is constant.
Proof By assumption | f(z) |  M for all z. M for all z.
Therefore, as before, | f '(z0) |  M / r0 for each z0 in the plane, and for any positive r0, no matter how large. M / r0 for each z0 in the plane, and for any positive r0, no matter how large.
It follows that f '(z0) = 0.
But z0 is arbitrary. Thus for all z, f '(z) = 0, and so f(z) = constant.
|
|
The Fundamental Theorem of Algebra
|
 |
 |
Theorem 5.7 (Fundamental Theorem) Any polynomial
P(z) = a0 + a1z + ... + anzn (an 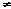 0) 0)
where n  1, has at least one zero. That is, there is at least one point z1 : P(z1) = 0. 1, has at least one zero. That is, there is at least one point z1 : P(z1) = 0.
It is curious that this important result has no easy algebraic solution.
Proof Suppose P(z) 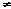 0 for any z. Then f(z) = 1/P(z) is entire. 0 for any z. Then f(z) = 1/P(z) is entire.
In fact f(z) is also bounded. For f is continuous and so bounded in any closed disk centred at the origin. Further, if R is large and z is exterior to the disk | z |  R, then R, then
| f(z) | = 1/| P(z) | 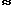 1/Rn (or worse!) 1/Rn (or worse!)
so f is bounded for all values of z in the plane. (We can tidy up this last argument, but the idea is that when | z | is large, so is | P(z) |.)
Now by Liouville's Theorem, f(z) and so P(z) is constant.
This contradiction shows that P(z) has at least one zero.
|
|
Factorization of Complex Polynomials
|
 |
 |
Let z1 be the zero guaranteed by the Fundamental Theorem.
Then P(z) = (z – z1)Q(z), where Q(z) is a polynomial of degree n – 1.
We deduce (by induction) that
P(z) = c(z – z1)(z – z2) ... (z – zn).
Corollary Any polynomial of degree n, where n  1 can be expressed as a product of n linear factors. That is, 1 can be expressed as a product of n linear factors. That is,
P(z) = c(z – z1)(z – z2) ... (z – zn),
where c and the zk are complex constants.
You might like to compare this result with what happens for polynomials over the reals R.
|