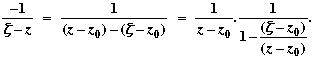|
A sequence z1, z2, ... , zn, ... has limit z if for all That is, we can make zn arbitrarily close to z by taking n sufficiently large. This definition is formally the same as for the real case. Of course, here the points of the sequence lie in the complex plane, rather than on the real line. The limit, if it exists, is unique. We say the sequence converges to z0 and write zn If there is no limit, we say that the sequence diverges. Theorem 6.1 If zn = xn + iyn (n = 1, 2, ...) and z = x + iy, then
Proof ( ( n > N1 So n > max(N1, N2) The expression z1 + z2 + z3 + ... is an infinite series. The set SN = z1 + z2 + ... + zN is a partial sum of the series. If the sequence S1, S2, ... , SN, ... converges to limit S we write The sum, when it exists, is unique. When a series does not converge, it diverges. Theorem 6.2 Suppose that zn = xn + iyn (n = 1, 2, ...) and S = X + iY. Then
Proof Let SN = XN + iYN denote the Nth partial sum, where XN = Now
by Theorem 6.1. Since XN, YN are the partial sums of In establishing that a given series has sum S, we define the remainder after N terms to be: RN = S – SN. Since | S – SN | = | RN – 0 |, SN Hence, a series converges to sum S We shall be particularly concerned with power series. a0 + where z0 and the an are complex constants, and z is any number (variable) in a stated region. We will use the notation S(z), SN(z), RN(z) for the sum, partial sum and remainder respectively. Theorem 6.3 (Taylor) Let f be analytic everywhere inside the circle C0 : | z – z0 | = r0. Then at each point z inside C0 f(z) = f(z0) + f '(z0)(z – z0) + f ''(z0)/2! .(z – z0)2 + ... + f (n)(z0)/n! .(z – z0)n + ... . That is, the power series converges to f(z) when | z – z0 | < r0. Notes (1) This is the Taylor series expansion about point z0. (2) If all terms are real, we get the real Taylor series. (3) The proof of Taylor's Theorem we give is remarkably ‘natural’, and is one of the rewards in our study of complex functions.
Now z lies inside C1, and f is analytic in and on C1, so by the Cauchy integral formula
Also for any complex c So Hence
We next integrate each term anticlockwise around C1, divide by 2 So Recall that | z – z0 | = r, | Thus if M denotes the maximum value of | f(
Since r/r1 < 1, So for each z interior to C0, the Taylor series for f converges to f(z). Let us seek the Maclaurin expansion for f(z) = ez. ez = 1 + z + z2/2! + ... + zn/n! + ... = Similarly sin z = z – z3/3! + z5/5! – ... , |z| < cos z = 1 – z2/2! + z4/4! – ... , |z| < sinh z = z + z3/3! + z5/5! + ... , |z| < cosh z = 1 + z2/2! + z4/4! + ... , |z| <
Let us try to find the Maclaurin series for the function Now This is not a Maclaurin series: the first two terms are unexpected, and function f has a singularity at z = 0. Question Perhaps there are other interesting series to investigate? Let C1, C2 be concentric circles, centre z0, with radii r1, r2 (r1 > r2). Theorem 6.4 (Laurent) If f is analytic on C1 and C2 and throughout the annulus between these two circles, then at each point in this domain, f(z) is represented by the expansion
where
each path of integration taken counter-clockwise. The series (*) is a Laurent series. (1) If f is analytic at all points in and on C1 except at z0, we can take r2 to be arbitrarily small. (2) If f is analytic at all points in and on C1, then
This means that (*) can be written
where
(4) In practice, some, or even many of the coefficients may be zero.
(5) For particular examples we usually do not find the coefficients of an expansion using the formula. In other words, the general formula is useful more as an existence formula.
If z lies in the annular region, then
This is the Cauchy integral formula extended to a multiply-connected domain.
Notice that by the Cauchy integral formula,
Comparing this equation with equation (†), the validity of (†) is confirmed. The first integral of (†) will give the Taylor series part, so as before

So from (†),
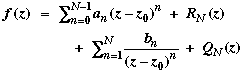
where an, bn are as given in the statement of the theorem, RN(z) is as before, and RN(z)
Also, Let M be the maximum of | f( This completes the proof of the theorem. There are many parallels with real series. This follows from the fact that Now if So the terms of a convergent complex sequence are bounded: that is, there exists M: | zn | < M for all n. We say that Thus We now prove an important result for power series. Analogues of the next results hold for Theorem 6.5 If a power series Proof Since Then | anzn | = | anz1n |.| z / z1 |n < Mkn. Now the series with terms Mkn (k < 1) is a real, convergent, geometric series. Our previous result shows that the set of all points inside some circle centred at the origin is a region of convergence for We note that by the theorem, the series cannot converge at any point z2 outside this circle. Similarly, if the series The theory starts to get a bit solid (boring!) here, so we settle for some stated results. Nevertheless, these results are important. Let S(z) = (1) Function S(z) is continuous at each z interior to C1. (2) Function S(z) is analytic at each z interior to C1. (3) If C is any contour interior to C1, then the power series can be integrated term by term, i.e.
[If C is a closed contour, then of course we get the value 0 on both sides.] (4) The power series can be differentiated term by term. Thus for each z inside C1, S'(z) = (5) The Taylor/Laurent series about z0 for a given function is unique.
(6) Let f(z) = If we formally multiply these series together and collect the coefficients of like powers of z, we get the Cauchy Product of the two series: f(z).g(z) = a0b0 + (a0b1 + a1b0)z + (a0b2 + a1b1 + a2b0)z2 + ... We now have: The Cauchy Product of two power series converges to the product of their sums at all points interior to their circles of convergence. For the next examples, set
This function is analytic everywhere except at z = 1 and z = 2. Find the Maclaurin series for f(z) valid in | z | < 1. Now Also | z | < 1
valid for | z | < 1. Thus this is the Maclaurin series for f(z) over the given domain. We are given
Find the Laurent expansion for f(z) in 1 < | z | < 2. In this case we have | 1/z | < 1 and | z / 2 | < 1. So
valid for 1 < | z | < 2. This is the required Laurent expansion. We observe here that c-1 (or b1) = 1. We noted in the previous calculation that c–1 (or b1) = 1. Recall that Thus
where C is any simple closed contour around the annulus (taken in the positive direction). That is,
This suggests the use of the Laurent series for the evaluation of integrals. Obtain the Laurent expansion in | z | > 2 for
Here | 2/z | < 1 and so | 1/z | < 1. So
valid for | z | > 2. Note that the coefficient of z-1 is zero. Hence Note It is possible to develop the whole theory of analytic functions beginning with series, but there is no great advantage. The proofs are not easy and motivation is lacking. If f is analytic at z0, there exists a circle centre z0 within which f is represented by a Taylor series: f(z) = a0 + where a0 = f(z0) and an = f (n)(z0)/n! . f '(z0) = 0 = f ''(z0) = ... = f (m -1)(z0) but f (m)(z0) f(z) = (z – z0)m = (z – z0)m g(z) say, where g(z0) = am Thus f(z) = (z - z0)m g(z) where g(z0) = am Since g(z) is represented by a convergent power series, g is continuous at z0. That is, given Now choose It follows that g(z) We have proved: Theorem 6.6 Let f be analytic at point z0 which is a zero of f. Then there exists a neighbourhood of z0 throughout which f has no other zeros, unless f
|
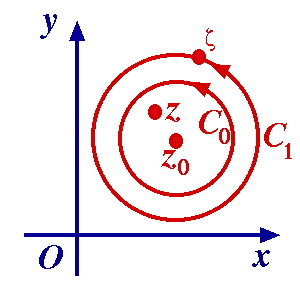 Proof Let z be any fixed point inside C0 and set | z – z0 | = r (so r < r0). Let C1 be a circle centred at z0 and having radius r1 : 0 < r < r1 < r2. Let
Proof Let z be any fixed point inside C0 and set | z – z0 | = r (so r < r0). Let C1 be a circle centred at z0 and having radius r1 : 0 < r < r1 < r2. Let 
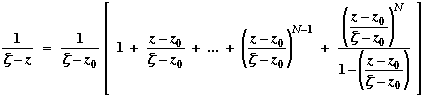
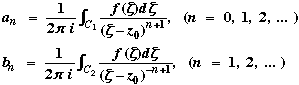 (**)
(**)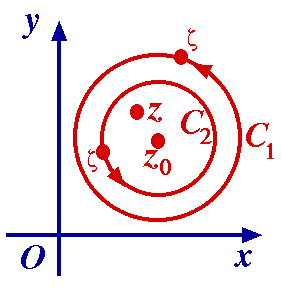 Then (*) is valid for 0 < | z – z0 | < r1.
Then (*) is valid for 0 < | z – z0 | < r1.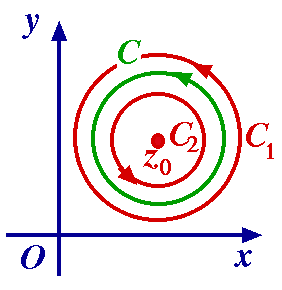 (3) Since f(z)/(z – z0)n+1 and f(z)/(z – z0)– n+1 are analytic throughout the annular region r2
(3) Since f(z)/(z – z0)n+1 and f(z)/(z – z0)– n+1 are analytic throughout the annular region r2  To show this explicitly in this special case, we take a small anti-clockwise directed circle K with centre z, lying within domain. Then
To show this explicitly in this special case, we take a small anti-clockwise directed circle K with centre z, lying within domain. Then