11. COAXIAL CIRCLES
|
|
Let us start with given points X, Y as double points of an involution on a line. Now if (P, Q) is a pair of mates in this involution, draw a circle on PQ as diameter. By choosing different pairs of mates, we thus obtain an infinite set of circles, and the points X, Y are inverse with respect to each circle of the system. |
P
Proof In the diagram, Now we need a new diagram ...
Proof If the circles are orthogonal, then AU is tangent to circle centre B, and so |
| Circles which cut each other at right angles are said to be orthogonal. In this case, the tangent to each circle at a point of intersection passes through the centre of the other – that is, it lies along the radius. |
We are given the blue system of coaxial circles with limiting points X, Y. Consider now another family of circles: the yellow circles passing through points X and Y. |
|
1. Three pairs of distinct points (P, P'), (Q, Q'), (R, R') are known to be mates in an involution. Show that the three involutions having (P, P'), (Q, Q'), (R, R') respectively as double points, have a pair of mates in common. |
P
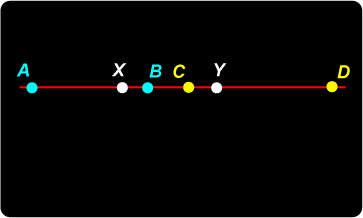 Exploring
Exploring 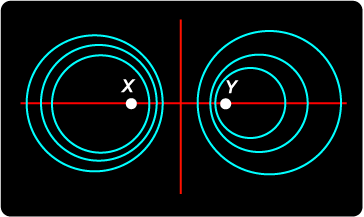 Coaxial Circles
Coaxial Circles Inverse Points and Orthogonality
Inverse Points and Orthogonality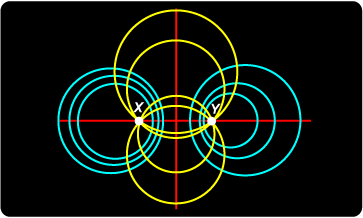 Orthogonal Circles
Orthogonal Circles