2. OUT OF INDIA     

There has been great interest shown over the centuries in magic squares.

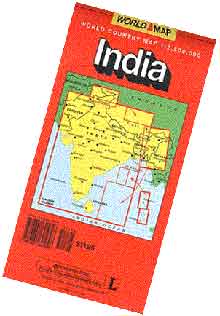
For example, the illustrated magic square below right comes from 11th Century India. Notice that the rows, the columns and the two diagonals each add up to 34.

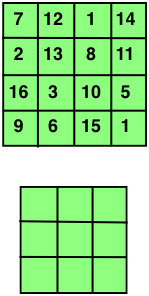
Your task is much simpler! See if you can place the numbers 1 to 9 in the 3 x 3 square illustrated at bottom rght so that the numbers in each row, in each column, and in each diagonal have the same sum.

Now you could do this by trial and error. Alternatively, perhaps you could calculate the common sum? Or determine the number which must be placed at the centre?

Hint 1

Suppose the square is completed. What is the sum of all the numbers? What is the row sum?

Hint 2

Look at the row, columns and diagonals through the centre square. Using the common sum, can you determine a value for the central number?

Solution

Let us assume that the numbers 1 to 9 have all been placed in the square. For the moment, we do not have to worry exactly where each number is placed. Now the total sum is given by

 1 + 2 + 3 + ... + 9 = 45.

This means that the numbers in row 1 plus the numbers in row 2 plus the numbers in row 3 add up to 45. If the row sums are equal, we deduce that the numbers in each row add up to 15. By the definition of magic square, this will also be the column sum and the diagonal sum. 

Next look at the row, column and two diagonals which pass through the central square. The sum of the elements contained in these is 4 x 15 = 60. Let C be the number in the centre. Now in obtaining the sum 60, we have used all the numbers surrounding the central square, and have counted C four times. That is, we have used all the numbers in the magic square and counted C an extra three times. Since the total sum is 45, this gives 45 + 3C = 60, so C = 5.

Now try putting some values in, starting with a 5 in the central square, and pairing numbers about the centre. A possible solution for the magic square has rows  6, 1, 8; 7, 5, 3;  2, 9, 4.

Extensions

1. Can you prove that the Indian magic square must have row sum 34? And that the four central squares must sum to 34?

2. In the 3 x 3 magic square, what happens if you add 1 to each number? Do we still get a magic square? Can you suggest how to place the numbers 2, 3, ... , 10 in a magic square? Extend this idea.

3. Can you place the numbers 2, 4, 8, 16, 32, 64, 128, 256 and 512 in a 3 x 3 multiplicative magic square? (The elements in each row, column, diagonal are to have the same product.)

Hint 1

Hint 2

Solution

Extensions