‘I don’t know,’ said farmer McQuill, looking wistfully at the many sheets of crumpled paper scattered over the floor. ‘I’m really having no joy with this problem.’
‘What is the problem?’ I asked.
‘Well,’ he replied, ‘I have this triangular block of land to divide equally amongst my three children. But I’m really hopeless when it comes to triangles.’
‘The solution is quite simple,’ I answered. ‘Simply divide one edge of the block into three equal parts, and join the points of subdivision to the opposite corner.’
‘I’m afraid it’s more complicated than that,’ said Farmer McQuill sadly. ‘There is a house placed on each corner of the block. Think how distressing it would be to have the bathroom fenced off from the rest of the house!’

What is the simplest way for Farmer McQuill to subdivide his property into three parts of equal area, in such a way that each part contains one of the houses?

Hint 1

This is obviously a triangle problem. Make a list of facts about triangles. What do you know about the altitudes? the medians? the perpendicular bisectors of the sides? the angle bisectors? Which of these facts is most likely to be useful here?

Hint 2

Text ...

Solution

It is known from geometry that the altitudes, the medians, the angle bisectors, and the perpendicular bisectors (mediators) of the edges of a triangle each meet in a common point. This leads to the possible sub-divisions (with unbroken lines) shown below.

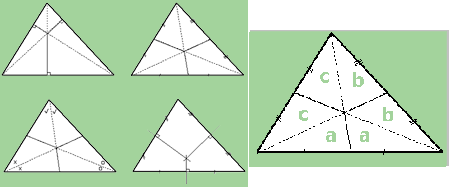
Now the three parts have to have equal area. Since we are not given the exact shape of Farmer McQuill’s land, we assume that the three parts will be equal for any triangle. Drawing various odd shaped triangles quickly convinces us that the median case is the one to look at. Here, the six small triangles have equal area. For it is clear that the triangles form pairs of equal areas a, b, c say (equal bases and same altitude). But now the larger triangles of areas a + 2c,  a + 2b have equal areas, so  b = c (= a similarly). This then gives the required solution.

Extensions

1. Could you solve Farmer McQuill’s problem if the houses were placed near the midpoints of the edges of the property?

2. Suppose Farmer McQuill had four children. Suggest a subdivision in which the four parts have equal area, and three of the parts each contain a house. Can you adapt this to give a fairer subdivision?

Hint 1

Hint 2

Solution

Extensions