 5. LEANING TOWERS
5. LEANING TOWERS 
The Prince of Pisa was somewhat concerned about the likely fall in tourist trade if the celebrated tower finally toppled. His great-aunt Florence had left him an enormous pile of bricks, but unfortunately, since the whole of Pisa was experiencing lean times, cement was impossible to get.
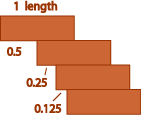
‘I wonder what sort of lean I could get by just stacking the pile of bricks,’ mused the Prince. ‘Let’s see. I can place this top brick (A) on the brick below (B) so that it just balances. That gives one half brick overhang. Now suppose I place bricks A and B on brick C so that they just balance ... .’
Assuming that the bricks are 0.25 metres long, will the Prince be able to match the four metre overhang of the present leaning tower? See the adjacent diagram.
You may like to try experimenting with a pack of cards.

Hint 1
How many terms must you take to make this larger than 0.5? 0.75? 1? 1.25? ...
Is there a pattern here?
Solution
Surprisingly, we can make the overhang as large as we please! This is one of those times in mathematics where intuition may not give the right answer. The top brick projects half a bricks length. The second projects a quarter, the third a sixth, the fourth an eighth, and so on. So adding bricks successively, the overhang is
1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/6 , 1/2 + 1/4 + 1/6 + 1/8,
and
1/2 + 1/4 + 1/6 + 1/8 + ... + 1/2n
for n + 1 bricks.
A calculator gives the values: 0.5, 0.75, 0.9166, 1.04, ... .
A standard pack of 52 cards will give an overhang of a little over 2.25 card lengths.
To see that the sum can be made arbitrarily large, we notice that
1/2 + 1/4 + 1/6 + 1/8 + 1/1 0 + ... + 1 /1 6 + ...
= 1/2 + 1/4 + ( 1/6 + 1/8 ) + ( 1/1 0 + ... + 1/1 6 ) + ...
> 1/2 + 1/4 + ( 1/8 + 1/8 ) + ( 1/1 6 + ... + 1/1 6 ) + ...
= 1/2 + 1/4 + 1/4 + 1/4 + 11/4 + ...
After the first term, additional values of 1/4 can be exceeded by taking 1 term, then a further 2 terms, then a further 4 terms and so on.
Extensions
1. Assuming that the weight of each brick acts at the centre (of gravity) of the brick, confirm that the sequence 1/2, 1/4, 1/6, 1/8 , ... of successive overhangs actually occurs.
2. Suppose that the Prince builds his tower with the successive overhangs being 1/2, 1/4, 1/8, 1/16, ... . Look up geometric series in your library or on the imternet, and show that the behaviour of this tower is quite different from the tower in the text.
Hint 1
Solution
Extensions


