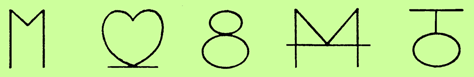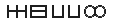Professor Topps was addressing the back wall of the lecture theatre as was his custom.

‘We all know,’ he said, ‘that a little knowledge is a dangerous thing, particularly at examination time.’

The students laughed nervously and tried to look more intelligent. ‘On the other hand,’ the professor continued, ‘sometimes it is not helpful to have too much knowledge either.’ The students relaxed again.

‘For example, when I write up the letters of the alphabet like this:’

A E F H I K L M ...
B C D G J ...

‘ – there is a very simple rule which I am sure you will be able to see immediately. Also, no doubt you can supply the next symbols in the following sequence of hieroglyphics.‘

Some of the students looked mystified, but some said ‘Aha!’

What is your reaction?

Hint 1

Look at the letters in the list.

What distinguishes the rows?

Hint 2

Do the hieroglyphics have any common pattern in their structure? Any symmetry?

Solution

There are two separate problems here, and each is likely to have an Aha! moment of recognition.

With the list of letters, the tendency is to make the problem harder than it is by looking for numerical patterns: one letter up, three letters down, one letter up ... . In fact the solution depends only on the shape of the letters: the top row contains letters with all straight components, the bottom row contains letters having a curved component..

Many people quickly spot the solution to the hieroglyphic problem, but can we work it out? The secret is to look for a common pattern of structure. In this case, each symbol is its own mirror image about a vertical mirror line. We now see that the half-images are 1, 2, 3, 4, 5, ... . So the next symbols would be 6 together with its mirror image, 7 together with its mirror image, and so on. In fact, the symbols are not uniquely defined, as there is some choice in the placing of the mirror lines.

Extensions

We observe that the hieroglyphics given above are just one example of writing either numerals or letters with reflections in horizontal or vertical mirror lines, or using a halfturn about a point. Unfortunately some of the capital letters have symmetry which makes them hard to disguise. Rather than writing a list, you might try to get someone to decode a message made up of suitable letters. For example HELLO could occur as:

  
 

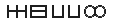
There is more scope with the list of letters. For example we might separate out letters containing loops, or letters containing T-junctions, or letters standing on pointed feet’. Another idea would be to separate out letters containing for example the ‘EE’ sound: B, C, D, E, G, ... . All that is needed is a logical rule.

Hint 1

Hint 2

Solution

Extensions