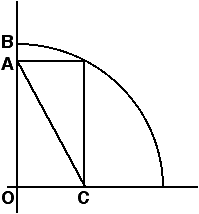
Here are two problems in geometry which have very simple solutions – if you can see them! In the upper diagram at right, the circle centred at O has radius 7. If AB = 1, how long is the line segment AC? And in the lower diagram, the large square has area 4. What is the area of the smaller shaded square? No lengthy calculations now!

Hint 1

Problem 1. Are all the obvious lines drawn in? Also beware of unnecessary information!

Hint 2

Problem 2. You might like to think of this as a jigsaw puzzle, with pieces which can be placed in different positions.

Solution

In the first problem, the most obvious line which has not been drawn is the other diagonal of the rectangle. Since a rectangle has equal diagonals, this will have the same length as AC. But we also observe that the new diagonal is also a radius of the circle, and therefore has length 7. It follows that AC = 7.

Notice that the information AB = 1 is not wrong, but it is unnecessary – the equation AC = 7 continues to hold for all values of AB between 0 and 7.

In the second problem, the large square is partitioned by the unbroken lines into the central shaded square and eight other pieces – two pieces along each side of the large square. Each two such pieces can be assembled to form a square which is the same size as the central shaded square. We can see this by rotating one of the pieces through a half turn about the midpoint of the edge of the large square which they share. Hence the large square is partitioned into the equivalent of five shaded squares

It follows that the large square has area five times that of the small shaded square. That is, the shaded square has area ⁴/₅ ^.

Extensions

^1. The first problem extends nicely to the 3-dimensional sphere, although the diagram is harder to draw!

^2. We can construct two analogues of the second problem using a 3 x 3 square grid. There are now two ways of constructing an inner square, using a 1 in 3 rule, or a 2 in 3 rule for the slopes of the defining lines. In each case, the question is the same: what is the area of the inner square? You will need to be flexible in your thinking to solve these, but the jigsaw method still works.

Hint 1

Hint 2

Solution

Extensions