 21. IN THE WET
21. IN THE WET 
Bob the berry farmer has an irregularly shaped flat block of land. Because he is not in the dried fruit business, he asks Allan his plumber friend to set up a sprinkler system.
Allan plans to fit one sprinkler at the midpoint of each of the sides. He will adjust each sprinkler so that the water just reaches the two adjacent corners. Allan shows Bob his sketch.
Bob is worried that some parts of the paddock will not be covered by the sprinklers. He draws his own sketch and shows it to Allan.
Now they are both worried, and looking for a third opinion – yours!

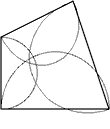
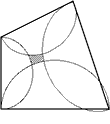
Allan’s Plan Bob’s Plan
Hint 1
Draw a fairly accurate sketch to determine what the likely answer will be.
Hint 2
The sketches involve semi-circular arcs. What properties of semi-circles do you know?
Solution
A careful sketch indicates that Allan’s solution may just be alright!
The geometrical property of the semi-circle which is required here, is that ‘any angle in a semicircle is a right angle’.
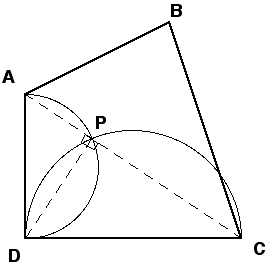
Label the quadrilateral property ABCD as in the diagram, and draw in the diagonal AC. Let PD be the perpendicular from D to AC. Then / DPC = 90° and / DPA = 90°. This means that point P lies on the semicircle DPC and on the semicircle DPA. In other words, these two watering arcs (just) cover the whole triangle ADC.
In the same way, the watering arcs based on sides AB and BC just cover triangle ABC. This shows that Allan’s plan works.
Extensions
1. It may seem strange that the diagonal AC passes through the point of intersection of the two drawn semi-circles. How does AC interact with the other two semi-circles?
2. Now experiment with the other diagonal. What happens here?
3. Is the shape of the quadrilateral important? Does Allans solution always work? Is there a quadrilateral for which point P lies on all the semi-circles?
4. Suppose that the lengths of the sides of the quadrilateral are a, b, c, and d. Can you find a nice upper bound for the area of the quadrilateral in terms of a, b, c, and d?
Hint 1
Hint 2
Solution
Extensions




