 22. LOST & FOUND
22. LOST & FOUND 
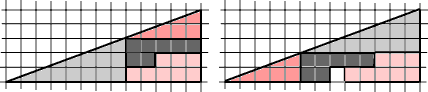
Carolyn looked pleased as she fitted the four puzzle pieces together to complete a triangle.
‘Now you try it,’ she said, turning to her friend Marilyn.
Marilyn quickly set to work, but soon stopped with a puzzled frown on her face.
‘That’s odd,’ she said. ‘There seems to be a square missing. I wonder where it has gone?’
Where has it gone?

Hint 1
Pictures can be deceiving!
Hint 2
You might look at the areas of
the pieces, or the slopes of
the oblique sides.
Solution
There is a working principle in mathematics that diagrams should never be used as a basis for proof. This problem is a good example.
Let us calculate the areas of the pieces. Measured in the squares of the underlying grid, we obtain 12 for the large triangle, 5 for the small triangle, and 7 and 8 for the remaining two pieces. This gives a total area of 32 squares in Carolyn’s solution, and 33 in Marilyn’s solution, counting the ‘missing’ square. The total expected area of the large 5 x 13 triangle is 32.5.
In fact in neither solution do the pieces fit together to form an exact triangle. In Carolyn’s solution, the hypotenuse angles in slightly; in Marilyn’s solution it angles out.
We can see this directly by calculating the slopes of the oblique sides. For the large 5 x 13 right triangle, the slope of the hypotenuse is 5/13 or approximately 0.3846. For the larger triangular piece the slope of the hypotenuse is 3/8 = 0.375. For the smaller triangular piece the slope of the hypotenuse is 2/5 = 0.4. Clearly in the assembling of the puzzle, these three hypotenuse cannot lie along the same line.
Extensions
1. Try constructing your own puzzle of this type. For example, take the outside puzzle shape to be a 5 x 3 right triangle. Take the pieces to be a 2 x 1 right triangle, a 3 x 2 right triangle, a 2 x 1 rectangle, and a 1 x 1 square. This does not make a good puzzle, because it is easy to see that the rearranged shapes are different. But it may help you understand what features are required for constructing a puzzle of this sort.
2. Now construct a puzzle of your own using a right triangle of larger dimensions.
3. Can you construct a similar type of puzzle which does not involve a right triangle for the outside puzzle shape?
Hint 1
Hint 2
Solution
Extensions


