26. SOME NEW
26. SOME NEW 
MATHS
The teacher looked at Ted’s arithmetic sheet. The answer was correct, but there was something suspicious about the working: Ted had simply cancelled the 6s, top and bottom.
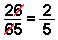
‘You can’t do that,’ growled the teacher. ‘You were just lucky you got the right answer. Look, suppose we take 49/98, and cancel the 9s, then we get ... . No! Ignore that example!
Let us take 16/64, and cancel the 6s. Now we get ... . Really, I don’t know where this new maths is leading us.’
There is in fact only one other ratio of two-digit numbers lying between 0 and 1 which simplifies correctly by such illegal cancellation. What is it?

Hint 1
Remember that a < c, and that a, b and c are all integers.
Hint 2
We need to investigate
ab/bc = a/c, remembering that ab stands for 10a + b.
Solution
We wish to solve the equation
10a + b = a .
10b + c c
Multiplying out gives 10ac + bc = 10ab + ac, or 9ac + bc = 10ab.
We need to find solutions for this equation for which a, b and c are single digits. This suggests we ‘solve’ for one of a, b, or c. Since we know that a < c, we try solving for b in terms of a and c. We obtain
b = 9ac / (10a – c ).
We now have to substitute values for a and c which make b an integer. We do this systematically, (discounting the trivial cases a = b = c ). For a = 3, 5, 6, 7, 8, 9 there are no non-trivial solutions. This leaves:
a = 1: c = 4, b = 6 (16/64 = 1/4);
c = 5, b = 9 (19/95 = 1/5).
a = 2: c = 5, b = 6 (26/65 = 2/5).
a = 4: c = 8, b = 9 (49/98 = 4/8).
Hence the only remaining fraction that gives the correct result with this illegal cancellation is 19/95.
Extensions
1. Investigate some other possible illegal cancellations.
For example, are the following ever valid?
ab/ac = b/c, ab/cb = a/c, ab/ca = b/c.
2. We could extend this investigation to quotients of 3 digits. One might expect this to be a harder problem!
Hint 1
Hint 2
Solution
Extensions