 28. GETTING THE /ANGLE
28. GETTING THE /ANGLE 
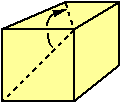
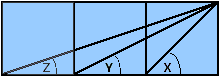
We have now two problems about angles.
The first is very simple. What is the angle between the two dotted lines in the cube illustrated above left?
Then the diagram above right shows three squares and three angles, X, Y and Z. By measuring the angles, it seems likely that X = Y + Z. Of course we can never prove this by measuring – there is always some margin for error. But there is a very pretty simple proof. Can you supply it? No trigonometry now!
Hint 1
In the first problem, what parts of the cube are hidden – not drawn in the sketch?
Hint 2
In the second problem, we want to show that angles Y and Z add to 45°. Perhaps we can place them so that they have a common edge?
Solution

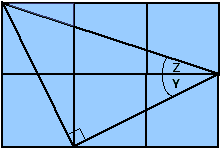
The solution of the cube problem becomes clear once we sketch in the hidden faces and one particular face diagonal. The three dotted face diagonals now form a triangle. The sides of this triangle all have equal length; hence the triangle is equilateral. It follows that the required angle is 60°.
You might like to compare this problem with the first problem in Aha! 14, where a significant line was also omitted.
For the second problem, we construct the isosceles triangle shown in this figure. The two shorter sides have the same length, and the marked angle is a right angle. Hence the triangle is a 90° – 45° – 45° triangle, and / Y + / Z = 45° ( = / X ) as required.
Why would we think of constructing this triangle? Firstly the problem is stated in terms of a square grid. And secondly, the angle sum is a nice commonly occurring quantity which suggests that there may be a simple solution.
Extensions
1. In the cube problem, we have constructed an equilateral triangle – a regular 3-sided polygon. Using the vertices of the cube can you construct a regular tetrahedron – a triangular based pyramid? Can you find two symmetrically placed such tetrahedra?
2. Look at the similar isosceles triangle inscribed in a 3 x 3 square grid. Can you generate a new problem from this? Or does this give a new solution to the original problem?
Hint 1
Hint 2
Solution
Extensions




