 30. FLORAL CIRCLES
30. FLORAL CIRCLES 
The professor and the barman peered at the three circles which the professor had made with his glass. Each circle passed through the centres of the other two.
‘Yes,’ the professor was saying, ‘I remember I once had this problem of trying to show that central overlapping (shaded) region has area greater than a quarter the area of each circle ... . ’The calculation was very complicated, and I don’t remember if I succeeded.’
‘Too hard for me,’ said the barman. ‘But it does remind me a little of those sunflower drawings we used to do as kids using a fixed compass.’
‘So it does,’ mused the professor.
A number of drinks later, he had completed a very pretty sunflower diagram, but unfortunately he was not then in any fit state to use it!
Make your own ‘sunflower drawing’ to determine easily whether or not the professor could have succeeded with his problem.
Solution
Draw sufficient circles to completely subdivide one of the circles which determines an arc boundary of the shaded region (see the diagram below).
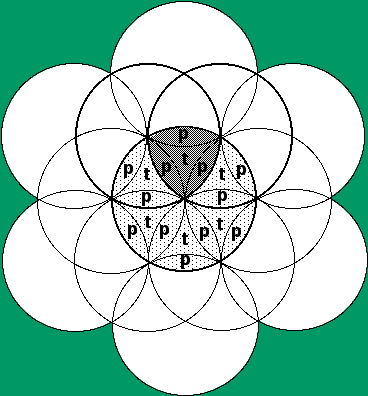
Let t denote the area of a ‘triangular’ region, and p the area of a ‘petal’.
Then in terms of t and p, the area of the circle is 12p + 6t. The area of the shaded region is 3p + t.
Since now 4(3p + t) = 12p + 4t < 12p + 6t, we have
3p + t < 14(12p +6t).
Thus the area of the shaded region is less than a quarter of the area of the circle, and the professor was wrong. In fact, the shaded region has 0.22 the area of the circle.
Extensions
1. The shaded region is surrounded by three ‘caps’, in which pairs of circles intersect. What can you say about the area of each of these?
2. What is the area of the three remaining outer regions? What area do you get if you combine one of these with a ‘petal’ region?
3. Without actually calculating areas, can you now determine which is the larger, t or p?



