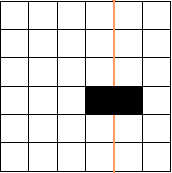
Suppose we want to cover a 5 by 6 area with 2 by 1 concrete tiles. Two possible ways are illustrated in the diagram. We notice that the first tiling has a ‘fault line’ which splits the large rectangle into two smaller ones. We therefore regard the second paving as preferable, and call it fault-free.

We now have three problems of increasing difficulty. Does there exist a fault-free tiling of

(a) a 2 by 6 rectangle?

(b) a 3 by 6 rectangle?

(c) a 6 by 6 square?

Where you cannot find a tiling, can you prove that one does not exist? (Logically, ‘I cannot find a tiling’ may not be equivalent to ‘A tiling does not exist’!)

Hint 1

In each case, sketch the area to be tiled, and look at different ways of laying the tiles.
How do the fault-lines occur?

Solution

We can show that fault-free tilings do not exist for any of the given rectangles. Any proof will do, but a nice proof is preferred!

(a) The 2 by 6 rectangle. No tile can be placed in a vertical position (like A in the diagram below), as this introduces a fault. If all tiles are placed horizontally, the central horizontal line becomes a fault line.

   

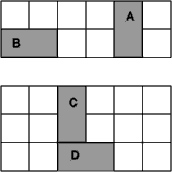
(b) The 3 by 6 rectangle. If the rectangle is tiled using only horizontal tiles, the rectangle will have two fault-lines. Consider then the possible placing of a vertical tile C. Such a tile can only occur at the end of the rectangle. For if not, one or other vertical edge of C, together with a vertical edge of tile D, will determine a fault-line.

Suppose then that the vertical tile C is placed in the top left corner of the rectangle, with D beneath. The tile next to D along the bottom must be horizontal (by the above argument), as must be the next tile. But now there is a horizontal fault-line.

(b) The 6 by 6 square. This square has 5 vertical lines and five horizontal lines, each of which must be crossed by a tile. In fact, each line must be crossed by at two tiles (or an even number), else an odd number of squares remains on either side of the line. But to cross each of ten lines with two tiles requires 20 tiles. But these would have a total area of 40– more than the area of the square! Hence there is no fault-free solution.

Extensions

We could try tiling non-rectangular shapes with 2 x 1 tiles. For example, suppose we have an 8 x 8 chess board with two opposite corner squares removed. Can we cover this with 2 x 1 dominoes?

Hint 1

 

Solution

Extensions