 39. A NASTY MATCH PROBLEM
39. A NASTY MATCH PROBLEM 
There are many problems which involve rearranging matches. Here is one which requires some ingenuity, but no trickery.

The 12 matches in the diagram enclose an area of five square units. Our problem is to arrange the matches to form a single simple boundary which encloses an area of four square units.
All the usual rules apply – no broken matches, crossing matches or matches left over.
You might think of solving this problem by forming a long narrow parallelogram for example, but then you would need a ruler to find the exact width. There is a region whose area of four units is easily determined.
Hint 1
Do we have to stay ‘on the square’?
Solution
It is easy to obtain regions of area 6, 7, 8 and 9 by keeping the matches ‘on the square’ and filling out the corners successively. Other possibilities are a 5 x 1 rectangle and a 2 x 4 rectangle, neither of which give the required area.
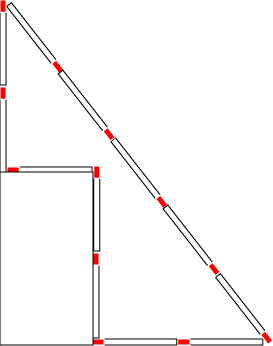
Hence it appears that we shall have to try a different approach. One idea would be to construct a right angles triangle, and in terms of the number of matches, the right angled 3 – 4 – 5 triangle is a suitable candidate. However, this triangle has area 6.
But as the diagram shows, a simple modification gives a region of area 4.
Extensions
1. Using 12 matches, we can easily obtain regions of area 4, 5, 6, 7, 8 and 9. Are there any other integral areas that can be easily obtained?
2. Use your knowledge of other Pythogorean triangles (right angled triangles with integral side lengths) to construct further problems of this type. (Unfortunately the areas and the numbers of matches rapidly get large.)
Hint 1
Solution
Extensions


